sytron, может, тогда вернитесь в начала ТВ и прорешайте задачки на тему "операции над событиями". Наподобие:
1. Пусть

- три произвольных события. Найти выражения для событий, состоящих в том, что из

a) произошло по крайней мере одно из этих событий;
b) все три события произошли;
c) ни одно событие не произошло.
2. Пусть
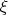
- некоторая случайная величина. Выразить
а) событие

"

" через события

"

",

"

";
b) событие

"

" через события

"

",

"

";
с) событие

"

- четное" через события

"

",

.
И, на всякий случай, чтоб потом не возвращаться, уделите внимание понятию несовместности событий и аддитивности вероятности.