Геометрия Лобачевского: когда четырехугольники изометричны?

[BVR]

Так эти полуокружности и строятся в верхней полуплоскости. Это же модель Пуанкаре.

-- Ср дек 21, 2011 22:32:06 --

Полуокружности с центрами на абсолюте и лучи с началом на абсолюте и перпендикулярные абсолюту - это прямые.

[Donald]

А равенство каких треугольников мне надо доказать?Этого и того,куда этот отобразится?

[BVR]

Я ж написал уже.
Если все вершины несобственные, то углы равны, а так ак и стороны равны, то четырехугольники равны.
Если две противоположные вершины $A$ и $C$, а у другого $A_1$ и $C_1$ несобственные, а две другие собственные, то проводим диагонали $BD$ и $B_1D_1$. Тогда треугольники $DAB$ и $D_1A_1B_1$ равны по первому признаку. Значит, существует изометрия, совмещающая эти треугольники. Вам осталось доказать, что если углы при собственных вершинах соответственно равны, то совместятся и другие стороны.
И самостоятельно рассмотрите третий случай, когда только одна вершина собственная.

[INGELRII]

Брр. Че-то как-то. Я правильно понимаю, что конгруэнтность фигур в геометрии Лобачевского возможна только при равенстве площадей двух фигур? Тогда мы строим два четырехугольника. У первого углы по часовой стрелке пусть будут $0, 0, 0, 0.$ У второго же они будут $0, \frac{\pi}{2}, 0, \frac{\pi}{2}.$ Все стороны у обоих этих четырехугольников будут бесконечными, против этого возражений нет? Однако площадь первого равна $2 \pi R^2$, а второго $\pi R^2$. И каким таким шаманством, спрашивается, можно первый совместить со вторым, чтобы площадь сохранилась?

[alcoholist]

BVR в сообщении #518009 писал(а):

при совмещении одной пары треугольников, совместится и другая пара

Вы уверены, что так произойдет?

Продолжение изометрий плоскости Лобачевского на ее границу на бесконечности (представленную как $\mathbb{R}\cup\infty$) это дробно-линейные преобразования

$$ x\mapsto \frac{ax+b}{cx+d}. $$

Такие преобразования транзитивны на тройках точек, но не на четверках.

Например, мы хотим перевести четверку $(0,1,2,3)$ в четверку $(0,\infty,2,s)$ ($s\in (0,2)$).
Очевидно, преобразование имеет вид

$$ x\to\frac{ax}{b(x-1)}. $$

Неподвижность $2$ дает $a=b$. И это самое $s$ может быть только $3/2$.

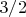
Ну... еще циклические перестановки вершин.

-- Чт дек 22, 2011 19:18:37 --

Можно и философски: множество идеальных четырехугольников образуют четырехмерное многообразие (надо из $(S^1)^4$ выкинуть все диагонали и по конечной группе профакторизовать). На этом многообразии естественно действует $PSL_2\mathbb{R}$. Фактор по этому действию -- одномерное что-то. Наверняка -- окружность. Вот точки фактора и будут классами изометричности.

[BVR]

alcoholist в сообщении #518574 писал(а):

Вы уверены, что так произойдет?

Уверен. Поскольку по одной из аксиом третьей группы (конгруэнтности) в данную полуплоскость от данного луча можно отложить только один угол равный данному.
Кроме того, если есть два равных треугольника, то существует единственное движение, переводящее один в другой (соответственно, конечно, поэтому циклич. не надо рассматривать). И собственную точку в несобственную оно перевести не может. Точку абсолюта в бесконечно удаленную может, но это тут не причем (или я не понимаю при чем оно тут :) )

[Donald]

Ребята,всем спасибо за помощь,сегодня сдал зачет,поэтому думаю что вопрос исчерпан)

[alcoholist]

Ок, давайте на пальцах.

Пусть имеется два идеальных четырехугольника. Вы отрезаете от одного идеальный треугольник и от второго. Они, разумеется, изометричны. Более того

BVR в сообщении #518593 писал(а):

если есть два равных треугольника, то существует единственное движение, переводящее один в другой

вот, единственное, назовем его $A$. Но пристроить четвертую вершину к идеальному треугольнику чтобы получился идеальный четырехугольник можно бесконечным количеством способов. Поэтому наше $A$ не обязано совмещать четвертые вершины.

... хотите, формулы напишу? Просто задам множество вершин четырехугольников, изометричных данному, как алгебраическое подмногообразие коразмерности 1 в $\mathbb{R}P^4$?

[BVR]

Мы же предполагаем, что углы $B$ и $D$ равны углам $B_1$ и $D_1$ соответственно. Поэтому, если часть их "закроется треугольником $A_1B_1D_1$, то оставшиеся части будут равны.
Или Вы хотите сказать, что если в двух четырехугольниках равны стороны и углы (соответственные), то четырехугольники могут быть не равными? Мне кажется, что это не так, но я подумаю...

[alcoholist]

Давайте так. Фиксируем две точки $B$ и $C$ на плоскости Лобачевского на расстоянии $a$ друг от друга. Для любого числа $b\in (a/2;+\infty)$ существует в точности две точки $A$, что $ABC$ -- треугольник с длинами боковых сторон $b$.

Но если $b=\infty$, то таких треугольников бесконечно много: любой треугольник $ABC$ с вершиной $A$ на абсолюте подойдет (среди них будет два вырожденных, у которых $A$ -- конец геодезической, на которой лежат точки $B$ и $C$).

[Munin]

alcoholist
Предлагаю отметить на идеальных треугльниках точки "середин сторон". Тогда будет очевидно, что склеить два таких треугольника по стороне можно разными способами.

[BVR]

alcoholist
Значит, получается, что к треугольникам, у которых по одной вершине лежит на абсолюте признаки равенства нельзя применять (стороны равны, а углы нет). Да они и не треугольники вообще-то. Ведь точки абсолюта не принадлежат плоскости Лобачевского.
Может тогда провести диагональ, через несобственные вершины

-- Сб дек 24, 2011 22:15:04 --

нет. Можно похожий контрпример привести..