Стационарные преобразования

динамической системы образуют полугруппу по операции композиции. Если они обратимы, то образуют группу.
Какую структуру образуют обратимые нестационарные преобразования

? Закон их композиции

записывается просто лишь для интервалов с общим краем, композиция любых других интервалов сразу выводит за границы двухпараметричности. Чем-то похоже на структуру прямоугольных матриц
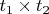
, для случая дискретного положительного времени.