Можно. Этого не заметили ни составители задач, ни я.
Чтобы у Вас не было сомнений, подробно излагаю ход рассуждения.
Имеется претендент на правильный ответ -- Выражение (с большой буквы, чтобы было ясно: именно следующее выражение):

Покажем, что добавление (

) к нему

не изменит его значения ни при каких значениях переменных.
От противного. Пусть в случае каких-то конкретных значений
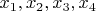
значение Выражения все-таки изменится после добавления к нему

. Это могло бы случиться двумя способами:
а) значение Выражения было равно

, а с

стало

;
б) значение Выражения было равно

, а с

стало

.
Вариант а) невозможен, так как

, независимо от

.
Вариант б) по свойствам "или" может иметь место лишь при

, что по свойствам "и" означает

и

. Сгруппируем вместе "слагаемые"

и

, уже входящие в Выражение:

Но тогда и Выражение равно

, что противоречит предположению б).
Итак, не существует случаев, при которых добавление к Выражению

изменяло бы его значение.
P.S. И даже так правильно:
