Проверьте пожалуйста правильно ли я нашёл смежные классы. У меня есть ощущение, что я не разобрался в этой теме.
Аддитивной группы

по подгруппе

:

Аддитивной группы

по подгруппе

: бесконечное количество множеств, в каждом из которых элементы с одинаковой дробной частью (не знаю как обозначить)
Мультипликативной группы

по подгруппе

чисел с модулем 1:

концентрические окружности
Мультипликативной группы

по подгруппе

:

, где

Мультипликативной группы

по подгруппе положительных вещественных чисел: аналогично предыдущему (?), только
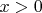
Аддитивной группы вещественных (3x2)-матриц по подргруппе всех матриц
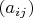
с условием

:
