Дисперсия суммы очков при бросании n костей. И пара вопросов

[farewe11]

Ну да, в принципе, подходит сюда дистрибутивность.. Спасибо за неравнодушие.

[_hum_]

farewe11, вы бы взяли какой учебник, систематизирующий знания по ТВ (с основами теории множеств и изложением в явном виде связи этой теории с теории вероятностей). Как вариант, Ширяев "Вероятность" или Лазакович "Курс ТВ".

[arseniiv]

(Оффтоп)

Joker_vD в сообщении #484275 писал(а):

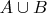
А на них рассказывают, что сумма событий обозначается $A+B$ или $A\cup B$, а произведение событий — $AB$ или $A\cap B$.

Кстати, я фанат теоретико-множественных обозначений для событий (хотя сначала как-то был против), но решил продолжить обозначения _hum_ для преемственности. Зря.

farewe11 в сообщении #484304 писал(а):

Почему это - и есть $A$?

Хотя вы уже во всём разобрались вроде, приведу картинку, которая мне нравится (не знаю, в который раз переизобрёл):



Весь прямоугольник — $\Omega = \bigsqcup_{i = 1}^5 D_i$. Части $A$, на которые оно делится полосками, — как раз $A \cap D_i$. Получается аналогичное предпредыдущему выражение для $A$.