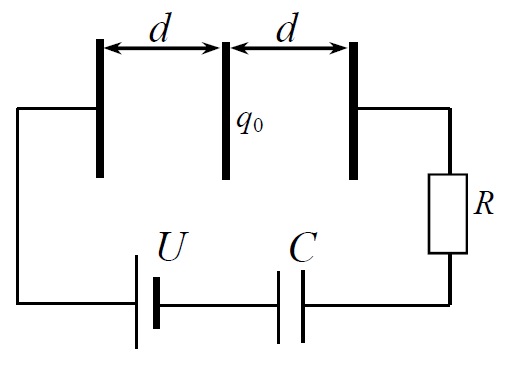
Три пластины площадью

расположены на расстоянии

друг от друга. Средняя пластина несет заряд

. Пластины подключены к источнику с напряжением

через резистор

и конденсатор

. Какую работу нужно совершить, чтобы очень медленно сдвинуть левую пластину на

вправо? Какое количество теплоты выделится при этом на резисторе?
Мое решение:
1) Емкость верхнего конденсатора:

Его можно представить как последовательно соединенные два конденсатора. Заряд на каждом -

Тогда, если заряд на нижнем -

то:

Отсюда

Тогда полная энергия в цепи:

2)После того как сдвигаем пластину, изменяется емкость верхних конденсаторов, но заряд на них не меняется. Новые емкости:

Тогда новый заряд на нижнем конденсаторе

:

Отсюда

Новая энергия:

Разница этих двух энергий:

А-работа по перемещению пластины.
Далее, т.к. заряд верхней системы не меняется, то напряженность поля внутри него постоянна =>

Дальше нам все известно, и можем найти

. Все верно?