Эйлер в 1749 году для доказательства не применял бесконечный спуск, а использовал лемму о существовании суммы двух квадратов двух взаимно простых чисел делящейся на это простое число.
Вы просто невнимательно читали это доказательство. Берём книжку А.В. Спивака (Арифметика-2, М.: Бюро Квантум, 2008) и читаем стр. 28-30: при доказательстве леммы 2 как раз и используется бесконечный спуск.
-- Вт авг 16, 2011 15:15:38 --Однако, моей целью было найти то «рассуждение, пролившее недостающий свет», которое по какой-то причине Ферма не посчитал нужным детализировать .
В Вашем рассуждении столько тумана, что ни о каком "свете" и речи быть не может.
В Вашей же рекомендованной литературе на стр. 17 которую Вы очевидно не дочитали до конца
http://mmmf.msu.ru/lect/spivak/summa_sq.pdf после доказательства леммы 2, которую Эйлер действительно доказал бесконечным спуском и на которую Вы ссылаетесь, есть еще и то, что в доказательстве теоремы Ферма о простом 4к+1 Эйлер не использовал эту лемму со слов .”...Осталось сослаться на теорему 2 — и
теорема Ферма–Эйлера доказана! Впрочем, Эйлер в 1749 году так не рассуждал, а
использовал следующую лемму.
Лемма 3. Если

— простое число, то существует сумма квадратов
двух взаимно простых целых чисел, делящаяся на

.
Доказательство:
В силу малой теоремы Ферма каждое из чисел

даёт при делении на p остаток 1. Следовательно, все разности

, где


, кратны

. Если ни одна из сумм

не кратна

, то все разности

кратны

и поэтому

при

; но многочлен степени

не может иметь
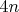
корней.”
-- 16.08.2011, 21:20 --Эйлер в 1749 году для доказательства не применял бесконечный спуск, а использовал лемму о существовании суммы двух квадратов двух взаимно простых чисел делящейся на это простое число.
Вы просто невнимательно читали это доказательство. Берём книжку А.В. Спивака (Арифметика-2, М.: Бюро Квантум, 2008) и читаем стр. 28-30: при доказательстве леммы 2 как раз и используется бесконечный спуск.
-- Вт авг 16, 2011 15:15:38 --Однако, моей целью было найти то «рассуждение, пролившее недостающий свет», которое по какой-то причине Ферма не посчитал нужным детализировать .
В Вашем рассуждении столько тумана, что ни о каком "свете" и речи быть не может.
В Вашей же рекомендованной литературе на стр. 17 которую Вы очевидно не дочитали до конца
http://mmmf.msu.ru/lect/spivak/summa_sq.pdf после доказательства леммы 2, которую Эйлер действительно доказал бесконечным спуском и на которую Вы ссылаетесь, есть еще и то, что в доказательстве теоремы Ферма о простом 4к+1 Эйлер не использовал эту лемму со слов .”...Осталось сослаться на теорему 2 — и
теорема Ферма–Эйлера доказана! Впрочем, Эйлер в 1749 году так не рассуждал, а
использовал следующую лемму.
Лемма 3. Если

— простое число, то существует сумма квадратов
двух взаимно простых целых чисел, делящаяся на

.
Доказательство:
В силу малой теоремы Ферма каждое из чисел

даёт при делении на p остаток 1. Следовательно, все разности

, где


, кратны

. Если ни одна из сумм

не кратна

, то все разности

кратны

и поэтому

при

; но многочлен степени

не может иметь
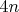
корней.”
Что касается тумана, я только путник в тоннелях Ферма, которые он пробил в горе Математика в нужные точки и пытаюсь разобраться, как это ему удалось сделать, стараясь использовать те суждения, которые использовались в его время.
-- 16.08.2011, 21:37 --Потому что

это тот же остаток, что и

, а

=

Потому, что для всех возможных квадратов остатки не квадраты.
Так много ответов

Но это должно вытекать как-то из предположения невозможности разложения

в сумму двух квадратов, иначе это неверно:
вот взял я

, а

- не получается.
И для

и для

остатки
по модулю 4 всегда квадраты, если

.
Все правильно, но мы же доказываем из противоположного, для любого простого

, предполагая, что оно не составляется из двух квадратов и, приходя методом спуска, именно к тем числам, о которых Вы говорите (наименьшее из них

?) как раз и доказываем о неверности нашего предположения.



