Задача. Пользуясь формулой Бернсайда, найти число существенно различных раскрасок граней куба в 3 цвета. (Две раскраски считаются существенно различными, если они не могут быть переведены друг в друга путём вращения куба.)
(Формула Бернсайда)
Пусть группа

действует на множестве

.
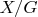
--- множество орбит,

--- множество неподвижных относительно

точек из

. Тогда

.
Я не понял, как находить

. Ведь если вручную считать, то не видно преимущества с ручным подсчётом числа раскрасок сразу... Вот, пускай не куб, а квадрат и не три цвета, а два. Тогда

--- множество раскрасок,

--- группа вращений квадрата (4 элемента: повороты на

; обозначим

),
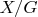
--- существенно различные раскраски.

, а остальные

я считал вручную. Наверное, можно проще?