Две волны называются параллельными, если направление их распространения параллельно.
И где вы вычитали такое определение?
Дело в том, что у волн, кроме направления распространения, есть ещё и другие геометрические характеристики, так что говорить "параллельны" без уточнений бессмысленно.
Учебники помогли со зверем разобраться, спасибо учебникам.
Назовите эти учебники, обманывающие читателя.
Для меня это пока загадка.
А вот с этим действительно могли бы помочь разобраться учебники.
Идея простая. Пусть первая интерферирующая волна приходит в точку интерференции в виде

тогда вторая, с разностью фаз
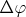
- в виде

Чтобы найти результат интерференции, мы раскладываем вторую волну по формуле суммы углов:

Здесь от времени зависят только вторые множители, а первые можно считать при них постоянными коэффициентами. Эти коэффициенты можно отложить на координатной плоскости вдоль двух перпендикулярных осей (одна ось так и называется

а вторая -

). Отсюда векторность.
Дальше сюжет развивается так. Первая и вторая волна складываются, получается (и по векторным правилам так же):


где


Когда

интерференция усиливающая, когда

- ослабляющая. Максимумы и минимумы приходятся на 2 и 0, это вы легко найдёте сами.
Зачем нужно раскладывать на слагаемые, пропорциональные

и

- несколько выходит за рамки сюжета, и я рассказывать не буду. (В матанализе выясняется, что эти функции в некотором смысле перпендикулярные, и поэтому могут быть использованы как единичные векторы декартовой системы координат.)



