Путаница здесь какая-то начинается. В случае матриц размера

базис состоит из

элементов, поэтому искомая матрица имеет размер
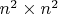
. В частности, матрица оператора транспонирования в пространстве матриц второго порядка будет иметь порядок

. В частности, для базиса, предложенного
выше, матрица

оператора транспонирования должна определяться из равенства

Причём, конечно, матрица

от элементов матрицы

зависеть не должна.