Ищу жорданов базис для матрицы

Собственное число одно:
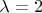
с алгебраической кратностью 3. Геометрическая кратность этого числа равна 2, так как ему соответствует два собственных вектора:

и

Жорданову форму найти-то легко. Раз геометрическая кратность равна 2, то будет две жордановы клетки, то есть ЖНФ имеет вид:

А потом я хочу найти матрицу перехода. Ищу её через присоединенные вектора. Для вектора, например,

, присоединенным (первого порядка) будет такой вектор

, что

. Для вектора

аналогично. Присоединенные вектора вместе с собственными образуют жорданов базис. Но проблема в том, что ни один из найденных собственных векторов не имеет присоединенных. Как быть?