Объясните пожалуйста эту теорему у меня написанно
Если функция

функция суммируема на E принадл

,то для почти всех
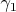
,она сумvируема по
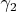
на

и при этом справедливо равенство

=

Обьясните пожалуйста что здесь значит
1)в левой части

2)

,

3)

4)Что значит суммируема на E понятным языком?
Заранее благодарен