Алгоритм
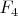
можно рассматривать как оптимизированную ("распараллеленную") версию алгоритма Бухбергера. Возможно, есть экзотические примеры, когда такая оптимизация будет вызывать замедление, но в целом она работает быстрее.
Чисто с практической стороны, с изобретением алгоритмов
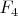
и

смогли построить базисы Грёбнера для задач, считавшихся практически недостижимыми для алгоритма Бухбергера. Например, т.н. HFE Challenge 1 (
подробности).
В этом смысле сравнивать
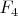
и

(а можно еще и

до кучи) между собой куда интереснее чем их же с алгоритмом Бухбергера.
Вот очень
неплохой обзор теории базисов Гребнера и алгоритмов Бухбергера,
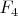
и

(с упором на применение к задачам криптографии).
Эмпирическое сравнение
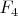
с другими алгоритмами есть также в исходной статье Фужера об этом алгоритме:
A new efficient algorithm for computing Gröbner bases (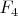 )
)


