Как называются эти группы? (типа SL_2(Z))

[Sonic86]

$SL_2(\mathbb{Z})$ - группа матриц $M$ $2 \times 2$ с элементами из $Z$ и с определителем $\det M = 1$.
$PSL_2(\mathbb{Z}) = SL_2(\mathbb{Z}) / \{ E, -E\}$. Для $SL_2(\mathbb{Z})$ тоже $\det M = 1$.
Можно рассмотреть аналогичную пару групп, отличающуюся только тем, что $\det M = \pm 1$ расширяющую эту пару.
Вопрос: как они называются, как обозначаются и где про них можно прочесть (в Винберге, Кострикине, ван дер Вардене и в гугле я не нашел). Как найти их ранг?

[zhoraster]

Называются они унимодулярными матрицами, обозначаются $GL_2(\mathbb Z)$. Насчет фактора не скажу.

[Sonic86]

zhoraster в сообщении #446044 писал(а):

Называются они унимодулярными матрицами, обозначаются $GL_2(\mathbb Z)$. Насчет фактора не скажу.

О! Действительно! И в гугле сразу нашел.

А фактор-группа $GL_2 (\mathbb{Z}) / \{ E, -E\}$ как называется?

[zhoraster]

Погуглив, нашел, что обозначают это дело $PGL_2(\mathbb Z)$ (и $PGL(2,\mathbb Z)$) и называют (сюрприз!) проективной линейной группой.

[Kallikanzarid]

Обычные матричные группы над свободными $\mathbb{Z}$-модулями (т.е. над свободными абелевыми группами).

[Sonic86]

zhoraster писал(а):

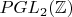
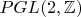
Погуглив, нашел, что обозначают это дело $PGL_2(\mathbb Z)$ (и $PGL(2,\mathbb Z)$) и называют (сюрприз!) проективной линейной группой.

Спасибо! Я бы ни в жисть не догадался Хотя все логично: опять проективной $G$ назвали фактор-группу группы $G$ по ее центру.

Kallikanzarid писал(а):

Обычные матричные группы над свободными $\mathbb{Z}$-модулями (т.е. над свободными абелевыми группами).

Ладно, тоже запомню.

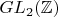
А как с рангом быть? Для $GL_2(\mathbb{Z})$ я нашел подгруппу из матриц вида
$\left\{ \bigl( \begin{smallmatrix} \pm 1& 0\\ 0& \pm 1 \end{smallmatrix} \bigr) ; \bigl( \begin{smallmatrix} 0&\pm 1\\ \pm 1 &0 \end{smallmatrix} \bigr) \right\}$
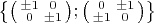
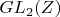
В ней 16 элементов, ее ранг равен 3, а значит ранг $GL_2(Z)$ тоже равен 3.
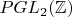
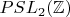
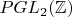
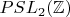
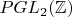
А вот для $PGL_2(\mathbb{Z})$ у меня сложно и недоделанно: я ищу базис в $PSL_2(\mathbb{Z})$, гомоморфизм $PGL_2(\mathbb{Z})$ в $PSL_2(\mathbb{Z})$, нахожу общий вид некоторого базиса в $PGL_2(\mathbb{Z})$ и там пытаюсь доказать, что он не базис, но полностью не получается...

[Kallikanzarid]

Sonic86 в сообщении #446057 писал(а):

Спасибо! Я бы ни в жисть не догадался Хотя все логично: опять проективной $G$ назвали фактор-группу группы $G$ по ее центру.

Вообще для матричной группы $G$ проективизация - это всегда $G/\pm 1$, хотя центр может быть и больше. Пример - $\mathrm{GL}(n, \mathbb{R})$, ее центр состоит из скалярных матриц.

(Оффтоп)

А что такое ранг?

[Sonic86]

Может в $PGL_2(\mathbb{Z})$ есть конечная подгруппа побольше, чем мой пример для $GL_2(\mathbb{Z})$?

-- Вс май 15, 2011 17:02:22 --

Kallikanzarid писал(а):

Вообще для матричной группы $G$ проективизация - это всегда $G/\pm 1$, хотя центр может быть и больше. Пример - $\mathrm{GL}(n, \mathbb{R})$, ее центр состоит из скалярных матриц.

Хорошо, буду знать (раньше не изучал это совсем).

Kallikanzarid писал(а):

А что такое ранг?

Это если $G = <S|R>$ - представление группы, то ранг $rk(G) = \min\limits_{S} \{ |S| \}$. Минимальное число образующих группы. Если не наврал. Сейчас проверю точно... Да, точно.

[Sonic86]

И еще хочу знать представление группы $GL_2(\mathbb{Z})$, какое-нибудь стандартное.

-- Вс май 15, 2011 18:29:55 --

Хе! Вот оно!:
http://mathoverflow.net/questions/46856 ... p-of-gl2-z