ТеорМех (выстрел из арт. орудия)

[Stotch]

Здравствуйте помогите пожалуйста решить задачку по теормеху
Из артиллерийского орудия стоящего на горизонтальной негладкой плоскости,производят
выстрел по горизонтальному направлению.Относительная скорость снаряда,когда он покинул дуло орудия равна v,масса снаряда $m$,масса орудия $M$,коэффициент трения об опорную поверхность $f$.Показать,что орудие откатится на расстояние $(\frac{mv}{M+m})^2\frac{1}{2gf}$
В примечании написано использовать теоремы о количестве движения,и о движении центра масс.
Я вообще не понимаю как это делается.Не могли бы вы по пунктам объяснить как это сделать?Может есть похожий пример подробно решенный?
Зарание благодарен

[Munin]

Stotch в сообщении #442382 писал(а):

Я вообще не понимаю как это делается.

А закон сохранения импульса в школе применять умели?

[Dan B-Yallay]

Цитата:

В примечании написано использовать теоремы о количестве движения,и о движении центра масс.

Приведите их тут.

[Stotch]

munin,нет я вообще не помню ничего из школы,какие действия выполнить по пунктам чтобы решить?просто вообще не понимаю.чтал книги тоже ничего не понятно.Может знаете похожий пример с подробным решением?

[мат-ламер]

(Оффтоп)

Кроме снаряда есть и заряд, который по массе сравним с массой снаряда. Заряд превращается в газы. Большая часть газов выталкивается по направлению полёта снаряда ( с той же скоростью). Меньшая часть газов возвращается дульным тормозом назад. После вылета снаряда назад идёт не всё орудие, а в основном ствол. Его движение относительно лафета гасится дополнительным тормозом. Сам же лафет вбит кольями в землю и практически не движется. Это я вспомнил сборы и гаубицу Д30. Извиняюсь за офф-топик.

Stotch. Для начала найдите начальную скорость орудия.

[Joker_vD]

Странно. Я решал задачу, и ответ у меня получился почти такой же, только в знаменателе не $M+m$, а просто $M$. Видать, где-то что-то в законе сохранения импулься проглядел...

[Stotch]

мат-ламер а по каким формулам?а что потом?воспользоваться теоремой о количестве движения?проосто в этом не понимаю вообще ничего

[мат-ламер]

Вероятно дело в том, что скорость снаряда измерялась относительно дула (ствола), а не относительно земли.

[Joker_vD]

мат-ламер в сообщении #442867 писал(а):

скорость снаряда измерялась относительно дула (ствола), а не относительно земли.

Хм. Тогда да, действительно.

Stotch, рассказываю возможный порядок действий:

1. Определиться с системой координат. Я предлагаю взять за начало отсчета $O$ точку на земле, где изначально стояло орудие, а за ось $OX$ — горизонталь, и направить ее по направлению полета снаряда. За нулевой момент времени — момент выстрела.
2. Записать закон сохранения импульса. До выстрела ничего не двигалось и суммарный импульс был равен нулю, а после выстрела он тоже равен нулю, потому что там все летит в разные стороны. В получившееся уравнение войдут: массы снаряда и орудия, скорости снаряда и орудия после выстрела относительно земли.
3. Используйте $\vec v_\text{снаряд отн. земли} = \vec v_\text{снаряд отн. орудия} + \vec v_\text{орудие отн. земли}$ и приведите подобные. Выразите $\vec v_\text{орудие отн. земли}$.
4. То, что получилось — это лишь начальная скорость орудия. Однако на движущеся орудие действует сила трения, которая вызывает ускорение, направленное противоположно начальной скорости. Это значит, что скорость орудия со временем уменьшается и в определенный момент станет равна нулю, после чего движение прекратится.
5. Найдите этот момент времени, используя следующую формулу: $\vec v(t) = \vec v_0 + \vec at$, где $\vec v_0 = \vec v_\text{орудие отн. земли}$, $a$ находится из второго закона Ньютона и выражения для силы трения $F_\text{трения} = Nf = Mgf$.
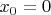
6. Орудие двигалось с момента выстрела и до момента останова (который вы нашли). Используйте $\vec x(t) = \vec x_0 + \vec v_0 t + \frac{\vec a t^2}{2}$, $x_0 = 0$; в качестве $t$ возьмите момент останова $t_\text{остан}$.
7. Длина $|\vec x(t_\text{остан})|$ и есть расстояние, пройденное орудием.

Разумеется, решать в векторной форме не стоит, достаточно работать с проекциями на $OX$.

[Парджеттер]

Переношу из "Помогите решить/разобраться (Ф)" в "Механику и Технику"

[Stotch]

Спасибо,попробую разобраться

[ewert]

Joker_vD в сообщении #442873 писал(а):

5. Найдите этот момент времени, используя следующую формулу: $\vec v(t) = \vec v_0 + \vec at$, где $\vec v_0 = \vec v_\text{орудие отн. земли}$, $a$ находится из второго закона Ньютона и выражения для силы трения $F_\text{трения} = Nf = Mgf$.
6. Орудие двигалось с момента выстрела и до момента останова (который вы нашли). Используйте $\vec x(t) = \vec x_0 + \vec v_0 t + \frac{\vec a t^2}{2}$, $x_0 = 0$; в качестве $t$ возьмите момент останова $t_\text{остан}$.
7. Длина $|\vec x(t_\text{остан})|$ и есть расстояние, пройденное орудием.

К чему все эти безумства?... Надо просто написать, что изменение кинетической энергии равно работе силы трения.

(Оффтоп)

мат-ламер в сообщении #442463 писал(а):

Кроме снаряда есть и заряд, который по массе сравним с массой снаряда

и т.д. Там просто опечатка: вместо "артиллерийское орудие" следует всюду читать "пушечка".

[Stotch]

ewert,обьясните пожалуйста по-подробнее а тоне разбираюсь совсем

[ewert]

После того, как пушка покатилась взад с уже вычисленной начальной скоростью -- пройденный ею путь, умноженный на известную нам силу трения (т.е. собственно работа силы трения) равен изменению её кинетической энергии (т.е. собственно кинетической энергии в начале движения).