Найти экстремали функцианала
![$\[
\begin{gathered}
\Phi = \int\limits_0^{x_1 } {\frac{{\sqrt {1 + (y')^2 } }}
{y}} \hfill \\
\left\{ \begin{gathered}
y(0) = 0 \hfill \\
y(x_1 ) = x_1 - 5 \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered}
\]$ $\[
\begin{gathered}
\Phi = \int\limits_0^{x_1 } {\frac{{\sqrt {1 + (y')^2 } }}
{y}} \hfill \\
\left\{ \begin{gathered}
y(0) = 0 \hfill \\
y(x_1 ) = x_1 - 5 \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered}
\]$](https://dxdy-02.korotkov.co.uk/f/1/6/5/165d23c67fdf869e88390f26980c1efe82.png) Решение.
Решение. Так как
![$\[
F = \frac{{\sqrt {1 + (y')^2 } }}
{y}
\]$ $\[
F = \frac{{\sqrt {1 + (y')^2 } }}
{y}
\]$](https://dxdy-03.korotkov.co.uk/f/6/f/7/6f78c6d5baa7789b0315af5fcae7085f82.png)
зависит только от
![$\[
{y,y'}
\]$ $\[
{y,y'}
\]$](https://dxdy-04.korotkov.co.uk/f/3/2/b/32bd505fa693c39ce7b2282fddb652c782.png)
, то уравнение Эйлера имеет вид
![$\[
F - y'F'_{y'} = c_1
\]
$ $\[
F - y'F'_{y'} = c_1
\]
$](https://dxdy-03.korotkov.co.uk/f/6/b/4/6b411f8985f54a4688c4139e23688b6a82.png)
или в нашем случаи
![$ \[
c_1^{} y^{} \sqrt {1 + (y')^2 } = 1
\]$ $ \[
c_1^{} y^{} \sqrt {1 + (y')^2 } = 1
\]$](https://dxdy-04.korotkov.co.uk/f/7/f/c/7fc08fc19f530d65ac867228351def4682.png)
Теперь возведём равенство в квадрат и разделяя переменные имеем
![$\[
\frac{{c_1^{} ydy}}
{{\sqrt {1 - c_1^2 y^2 } }} = dx
\]$ $\[
\frac{{c_1^{} ydy}}
{{\sqrt {1 - c_1^2 y^2 } }} = dx
\]$](https://dxdy-04.korotkov.co.uk/f/b/7/d/b7dd56fe3351554dc68ac1a8ff2449bc82.png)
Решая данное д\у имеем
![$\[
y = \frac{{\sqrt {1 - c_1^2 (x + c_2 )^2 } }}
{{c_1 }}
\]$ $\[
y = \frac{{\sqrt {1 - c_1^2 (x + c_2 )^2 } }}
{{c_1 }}
\]$](https://dxdy-02.korotkov.co.uk/f/d/a/2/da28c98423bc2403eee9599c3277caa582.png)
Теперь необходимо найти константы
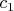
и

Здесь и возникает вопрос, вот скажем одно равенство можно взять из того, что

а вот второе где взять?