Найти предел.

[bundos]

Пусть $f(x): \mathbb{R}\rightarrow(0;\infty)$, дифференцируемая функция для которой $\lim\limits_{x\to\infty} f(x)=\infty$ и $f'(x)$-ограничена.
Пусть $F(x)=\int\limits_{0}^{x}f(x)dx$. Последовательность $\{a_n\}$ задана рекуррентно: $a_0=1, a_{n+1}=a_b+\frac1{f(a_n)}$ и последовательность $\{b_n\}$ такая, что $b_n=F^{-1}(n)$. Доказать, что $\lim\limits_{n\to\infty}(a_n-b_n)=0$
Подскажите пожалуйста, как подступиться к этой задаче.

[ИСН]

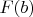
Мне кажется так. Вот есть два числа, a и b - не n-тые, а просто сами по себе, два мрачных числа без прошлого, без паспортов, только со справками об освобождении. Теперь мы что делаем. К a прибавляем $1\over f(a)$. К b прибавляем столько, чтобы $F(b)$ возросло на единичку. Говорят, от этого они чуть-чуть сблизятся.
Врут?

[myra_panama]

bundos в сообщении #433431 писал(а):

$a_0=1, a_{n+1}=a_b+\frac1{f(a_n)}$

Это , что рекуррентное посл...?

Не ужели так : $a_0=1, a_{n+1}=a_n+\frac1{f(a_n)}$ ?

[bundos]

$a_0=1, a_{n+1}=a_n+\frac1{f(a_n)}$, пардон, опечатался...