Конечно. Главный вопрос , на мой взгляд, в диске или моторе , который вращает диск. Можно ли подобрать такой радиус диска, чтоб исключить стопор? Безусловно . Возьмем, к примеру, длину бруска 100 м, а высоту 1000м. По предложенной формуле получится что- то несусветное. Однако ж подобрать диаметр диска , иначе говоря дать нужный момент на диск можно- и никакого стопора не будет. Это говорит о том, что сила трения в данном примере так не рассчитывается.
Представьте, что у Вас не диск и брус, а зубчатое колесо и зубчатая рейка (аналог
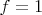
).
В этом случае в предлагаемой Вами схеме, какой бы Вы диаметр зубчатого колеса не применили, какой бы крутящий момент не приложили к колесу, стопор не устраните (естественно, если не войдете в область упругих или пластических деформаций, но это будет уже другая история).
Если же

будет малым, таким, что

, то тогда будет иметь место проскальзвание.
Другими словами, в заданной схеме (при неизменных размерах

) все зависит от коэффициента трения, который в свою очередь зависит только от комбинации используемых материалов (сталь-по дереву, алюминий-по фторопласту, резина-по стеклу и т.д.).
Но еще раз повторюсь. Если нам по условию задачи предстоит определить поведение бруса, то необходимо именно к нему прикладывать внешние нагрузки. Я имею в виду направление

и

. По модулю они, что для диска, что для бруса одинаковы (3-й закон Ньютона).