ЦПТ здесь всё-таки никак не применима, я был не прав.

не равна n дисперсий, и вообще, предположение, что N достаточно большое, чтобы не считать его случайной величиной - слишком большая натяжка даже для идеи доказательства.
Попробовал через характеристические функции:



Тем временем хар. функция для нормального распределения:

В случае стандартного нормального распределения:

Никакой сходимости с ростом

я не вижу.
Я с самого начала пытался расписать всё напрямую, как
_hum_ . И дошел до того же места... Как действовать дальше непонятно. Непонятно, как оценить
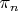
и модуль разности в правой части неравенства.
-- Пн фев 28, 2011 18:51:37 --Существует такая теорема ("ЦПТ для пуассоновских случайных сумм"):
Цитата:
Рассмотрим

— независимые одинаково распределенные случайные величины.
Пусть

(конечное),

(тоже конечная).

;

и

независимы

.
Тогда при

выполняется

.
Если в неё подставить мои исходные данные (нулевое мат.ожидание и единичную дисперсию), то из этой теоремы вытекает доказываемая мною сходимость. В принципе, этого достаточно. Осталось только научиться доказывать эту самую теорему.
Но преподаватель говорил, что задача очень простая, делается как-то элементарно. Причём нужно учесть, что лямбда в условии - натуральное число. Это вроде как упрощает доказательство.
Будет здорово, если удастся обойтись без "ЦПТ для пуассоновских случайных сумм".



