Можно так доказать счётность рациональных. Сначала покажем счётность неотрицательных рац. чисел. Высотой несократимой дроби (рац. числа) назовем сумму числителя и знаменателя. Очевидно, что кол-во неотрицательных рац. чисел с определенной высотой конечно, и что высота определятся однозначно для любого рационального числа. Тогда все неотрицательные рациональные числа можно упорядочить так:

(высота 1);

(высота 2);

,

(высота 3);

,

(высота 4);

,

,
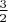
,

(высота 5); ...
Далее после каждого члена последовательности (кроме нуля) добавляем соответствующее отрицательное число. Q.E.D.



