Да , совершенно верно - это утверждение неверно.
Отлично.
Я сейчас напишу доказательство, а Вы скажете, где ошибка.
Будем обозначать машину, задаваемую программой

символом

.
1. Допустим, требуемая машина существует. Обозначим эту машину

.
Напомню, что мы хотим, чтобы выполнялось следующее:
а)

- не программа =>

б)

останавливается =>

в)

не останавливается =>

2. Построим на основе программы машины

программу для другой машины

, которая принимает один параметр-строку, и работает следующим образом:
Если

, то

завершает работу.
Если

, то

продолжает работу бесконечно.
При желании я могу явно выписать преобразование программы машины

в программу машины

. Надеюсь, Вы можете и сами это сделать.
3. Обозначим программу машины

буквой

, т.е.

. Рассмотрим значение

.
Значение

зависит от значения

. Рассмотрим каждый из трех случаев:
а) случай (а) реализоваться не может, т.к.

является программой некоторой машины.
б) пусть

останавливается. Тогда

и

зацикливается. Т.к.

, получаем

останавливается =>

не останавливается.
в) пусть

не останавливается. Тогда

и

останавливается. Т.к.

, получаем

не останавливается =>

останавливается.
В итоге получаем:

не останавливается <=>

останавливается.
Противоречие.
Здесь, ошибка в выражении

Если в качестве первого параметра вы можете подставить "голый алгоритм", то в качестве второго - это уже будет неверно, поскольку входной параметр для этого есть алгоритм вместе с другим входным параметром.
Т.е.

Для следующей подстановки (если вы переопределяя переменные пытаетесь вновь подставить весь этот алгоритм в A) вы получите

а вовсе не превоначальный вариант

который ,вообще говоря, тоже некорректен, поскольку не было указано, какой самый первый параметр используется в x.
Т.е. пока полностью не сформирован алгоритм A (не указано, какие в него будут передаваться параметры, иначе, этих параметров в природе не существует) нельзя создать и алгоритм B.
Если же вы, создадите "незавершенные" алгоритмы A и B и только только потом так перенаправите ссылки, чтоб они друг друга циклически вызывали, то это у вас будет всего лишь зацикленный код.
Программу с зацикленным кодом можно считать некорректной, которая никогда не завершится.
Поэтому достаточно вставить в одном из участков блок, отлавливающий ситуацию возникновения бесконечных циклов и выводящий после этого конкретный результат (0), как все неопределенности сразу пропадут.
Кроме того есть еще одно место ,где можно указать на ошибку, это:
"Построим на основе программы машины

программу для другой машины

, которая принимает один параметр-строку"
Здесь указано , что в качестве параметра передается строка.
Но в этой строке должно быть упакован не только сам код, но и те параметры ,которые в этот код будут переданы.
А код+параметры никогда не будут равны только коду.
Т.е. опять же ситуация

никогда не может быть реализована.
Тут же по умолчанию считается, что как только некоторые параметры будут переданы в алгоритм B, так они сразу "волшебным образом" модифицируют код алгоритма A так, что эти же параметры будут переданы в него, в качестве исходных, когда , на само деле должна произойти цепочка передач параметров, В конце которой никак не может оказаться ситуация

.
Еще одно ,последнее возражение:
Ошибка типов: Ведь сказано же что в


- это код, а
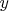
-это его параметры.
Здесь же производится передача ,в качестве первого параметра, код+параметры либо код без параметров, что есть нарушение условия.
PS
Это то , что я сходу смог найти.
Потом выберу один окончательный вариант.
-- Ср янв 26, 2011 16:42:26 --Я никогда не говорил, что множество рациональных чисел (рациональная система счисления) самая лучшая - я говорил, что она самодостаточная.
Что это значит? Факт заключается в том, что нельзя указать рациональное число,
в точности равное

. Это и означает, что

-
иррациональное число.
Как называть - это уже другой вопрос.
Вы это называете иррациональным числом, я - алгебраическим.
Но для того чтоб доказать, что существует такое множество "иррациональных чисел" - недостаточно доказать, что есть числа, которые не равны рациональным.
Я под множеством "иррациональных чисел" подразумеваю те числа, которые не равны рациональным и ... их количество несчетно.
Т.е. надо еще доказать несчетность иррациональных чисел.
Если нет - то эти числа так и останутся алгебраическими - и будут всего лишь одной из систем позиционирования на множестве "алгоритмических" чисел.
Число которых хоть и счетно ... но для них невозможно создать единую универсальную систему позиционирования.
Поэтому надо выбирать какой-то неидеальный вариант и рациональные числа - один из таких вариантов.



