



_ therefore _

.... и так далее.
Вопрос, почему мы можем сложить уравнение (2) + (3)?
Ведь чтобы найти точку пересечения, их нужно приравнять?
т.е. как это понять интуитивно?
-- Ср янв 26, 2011 05:44:20 --и еще у меня такой вопрос

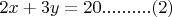
можно ли к (2) прибавить 5, чтобы избавиться от 8y?
Просто я в примерах везде вижу только умножение и деление каждого коэф-ента.
т.е.
5 + (2):
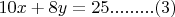
(1) + (3):


правильно?