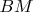Если обозначить синий треугольник PQR, то получается, что вектор PQ имеет координаты:

,
а вектор PR имеет координаты:
 -- Вс янв 16, 2011 20:21:37 --
-- Вс янв 16, 2011 20:21:37 --Не. Что-то у Вас не то с координатами. Я с derive делаю.
Да! то, что я написал - это без множителя

(и там и там)
Так вот площадь

равна

модуля определителя, составленного из координат этих векторов. А он равен (без учёта этих множителей

)

(так говорит Дерайв). А, значит, если учесть эти множители, то получим

. А площадь исходного треугольника равна

. Ч. т. д.
-- Вс янв 16, 2011 20:24:08 --ЗЫ

из первой строки;

из второй строки и перед определителем
 -- Вс янв 16, 2011 20:28:33 --
-- Вс янв 16, 2011 20:28:33 --Самое странное, что я нигде не использовал ограничения на

и


Это, что ли означает, что можно брать чевианы, падающие и на продолжение сторон?

А, кстати, видимо даже не надо выделять случай, когда эти чевианы в одной точке пересекаются - типа, и пусть себе пересекаются
 -- Вс янв 16, 2011 20:32:49 --
-- Вс янв 16, 2011 20:32:49 --Ещё я забыл уточнить, что

- середина

;

- середина

;

- середина