Пытаюсь понять условие и, если получится, впоследствии решить следующую задачу:
Пусть

- оператор, который переводит подмножества множества

в подмножества множества

, и
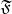
- семейство всех таких множеств, что

. При каких условиях
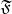
будет топологией, а

(одновременно) - оператором перехода к ядру?
Во-первых, мне непонятно, что такое "оператор перехода к ядру"? Он имеет какое-то отношение к ядру линейного оператора? Во-вторых,
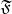
- это семейство открытых множеств, стало быть

означает, что открытые множества переходят сами в себя, но ведь нигде не говорится (текст условия приведен дословно), какие именно подмножества носителя

мы считаем открытыми? Размышляя по смутной аналогии с ядром линейного оператора, следует ли предполижить, что

переводит множества, не являющиеся открытыми в

?
Зранее спасибо за любые идеи!