Binomial sum(2)

[man111]

Prove that
$1-2n+\frac{2n(n-1)}{2!}-\frac{2n(2n-1)(2n-2)}{3!}+......................+\frac{(-1)^n2n(2n-1)....(n+2)}{(n-1)!}=\frac{(-1)^{n+1}(2n)!}{(n!)^2}$

[caxap]

Если вы хотели написать

man111 в сообщении #392348 писал(а):

$1-2n+\frac{2n({\color{blue}2n}-1)}{2!}-\frac{2n(2n-1)(2n-2)}{3!}+......................+\frac{(-1)^{{\color{blue}n-1}}2n(2n-1)....(n+2)}{(n-1)!}$

то $\frac{2n(2n-1)\cdots (2n-(k-1))}{k!}=\frac{(2n)^{\underline{k}}}{k!}=\binom{2n}{k}$, т. е. ваша сумма: $\sum_{k=0}^{n-1} (-1)^k\binom{2n}{k}$. Рассмотрим последовательность $\langle (-1)^k \binom{2n}k\rangle_k$ и последовательность единиц $\langle 1\rangle$. Производящая функция для первой -- $(1-z)^{2n}$ (бином Ньютона), для второй -- $1/(1-z)$ (геометрическая прогрессия). Их свёрткой будет последовательность частичных сумм первой последовательности, а ПФ будет $\frac{(1-z)^{2n}}{1-z}=(1-z)^{2n-1}$. Её коэффициент при $z^{n-1}$ и будет искомой суммой. По биному Ньютона: $(-1)^{n-1}\binom{2n-1}{n-1}=(-1)^{n-1} \frac{n}{2n}\,\binom{2n}{n}=\frac 12 (-1)^{n+1} \binom{2n}{n}=\frac 12 (-1)^{n+1} \frac{(2n)!}{(n!)^2}$.

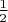
У меня почему-то $\frac 12$ вылезла. Может где-то ошибся. А может опечатка у вас.

-- 27 дек 2010, 17:48 --

(Оффтоп)

Хотя, скорее у вас:

In[2]:= Sum[Binomial[2n,k] (-1)^k,{k,0,n-1}]
              n
        -((-1)  Binomial[2 n, n])
Out[2]= -------------------------
                    2

А может я просто неправильно понял изначальную сумму. Проверьте, пожалуйста, задание на опечатки.

[man111]

Thanks caxap..

[EtCetera]

Надо сказать, что рассматриваемое тождество
$\sum\limits_{k=0}^{n-1}(-1)^k\binom{2n}{k}=\dfrac{(-1)^{n+1}\binom{2n}{n}}{2}$
можно доказать гораздо проще.
Заметим, что $\sum\limits_{k=0}^{n-1}(-1)^k\binom{2n}{k}=\sum\limits_{k=n+1}^{2n}(-1)^k\binom{2n}{k}$, т.к. $(-1)^k=(-1)^{2n-k}$ и $\binom{2n}{k}=\binom{2n}{2n-k}$. Тогда
$0=(1-1)^{2n}=\sum\limits_{k=0}^{2n}(-1)^k\binom{2n}{k}=2\sum\limits_{k=0}^{n-1}(-1)^k\binom{2n}{k}+(-1)^n\binom{2n}{n}$,
откуда со всей очевидностью следует доказываемое равенство.

(Cпециально для caxap)

Более сложный вариант (подозрительно напоминающий Ваше доказательство ):

$$\sum\limits_{k=0}^{n-1}(-1)^k\binom{2n}{k}=\frac{(-1)^{n+1}}{(n-1)!}\sum\limits_{k=0}^{n-1}\binom{n-1}{k}\frac{(2n)!}{(2n-k)!}\cdot(-1)^{n-1-k} (n-1-k)!=\frac{(-1)^{n+1}}{(n-1)!}\sum\limits_{k=0}^{n-1}\binom{n-1}{k}\left.\left(x^{2n}\right)^{(k)}\right|_{x=1}\cdot\left.\left(x^{-1}\right)^{(n-1-k)}\right|_{x=1}=$$

$$=\frac{(-1)^{n+1}}{(n-1)!}\left.\left(x^{2n}\cdot x^{-1}\right)^{(n-1)}\right|_{x=1}=\frac{(-1)^{n+1}}{(n-1)!}\left.\left(x^{2n-1}\right)^{(n-1)}\right|_{x=1}=\frac{(-1)^{n+1}}{(n-1)!}\cdot\frac{(2n-1)!}{((2n-1)-(n-1))!}=\frac{(-1)^{n+1}}{2n!}\cdot\frac{(2n)!}{n!}=\frac{(-1)^{n+1}\binom{2n}{n}}{2}$$

Здесь использовалось тождество $(-1)^m\cdot m!=\left.\left(x^{-1}\right)^{(m)}\right|_{x=1}$.

P.S. Извиняюсь за легкий приступ некрофилии.