Здравствуйте. Не получается решить задачу по урматфиз из сборника Бицадзе.
решить задачу Коши
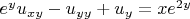

Вот начало моего решения, не знаю как продолжить и вроде ошибка в нахождении общего решения.
Находим замену переменных, через ура-я характеристик:

Так как

Приведем к каноническому ввиду:
Пусть

.

Подставим производные в уравнение и получаем:

После сокращения:

Дальше как я понимаю нужно полученное уравнение проинтегрировать по

и получим общее решение? я просто не знаю как это сделать( .
Заранее спасибо.