Раскрашивание квадрата (прога или мозг?)

[Xenia1996]

Сколькими способами можно в квадрате NxN клеток закрасить некоторые клетки так, чтобы в каждой строке и в каждом столбце оказалось ровно по n закрашенных клеток?
Надо прогу писать, или можно до формулы додуматься?

[MrDindows]

$N$ и $n$ - числа разные?)

[Sonic86]

Все-таки правильно:
$K(N,n)$ - число раскрасок
$K(N,1) = N!$ $K(N,N) = 1$ $K(N,n) = K(N-n)$
хотя бы это
решать лучше мозгом

[ИСН]

MrDindows в сообщении #389825 писал(а):

$N$ и $n$ - числа разные?)

Мелькнула мысль сказать:
"Пишите прогу. На Паскале"

[caxap]

Sonic86, ну это только "концы" рекурсии. Вся сложность -- в самом рекурсивном шаге. (Я лично дальше этих концов не продвинулся.)
MrDindows, а какой интерес с $n=N$? Конечно разные.

[age]

По-моему, это как-то должно быть связано с определителями, в частности, $K(N,1)$ - сколько миноров $N-1$-го порядка может быть у квадратной матрицы $N\times N$

[Sonic86]

(Оффтоп)

сахар писал(а):

Sonic86, ну это только "концы" рекурсии. Вся сложность -- в самом рекурсивном шаге. (Я лично дальше этих концов не продвинулся.)

Я тоже Я хотел поддержать идеологию "мозг вместо проги" и попытался показать, что тут хоть что-то можно решить

[venco]

A008300

[arseniiv]

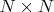
Кстати, эта задача случайно не имеет ничего общего с латинскими квадратами? Например, возьмём латинский квадрат $N \times N$ и числа $1, \ldots , n$ в его клетках отождествим, а остальные выкинем. Можем ли мы получить таким способом все нужные нам закрашивания (разумеется, будут и лишние повторяющиеся), или какие-то нельзя получить? (Разумеется, от этого легче вычислять незивестные члены A008300 не станет, но просто интересно. Хотел перед сном подумать о доказательстве или опровержении, но путного ничего в голову не пришло. Кажется, что верно.)