Хотелось бы выяснить, насколько верны и строги мои рассуждения относительно некоторых моментов:
Итак, нужно найти точки ветвления функции

.
Точки

,
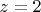
- точки ветвления (первая за счет логарифма, вторая за счет корня), это я доказал.
Вопрос вызывает третья точка:

.
С одной стороны, эта точка будет точкой ветвления для

, т.е. в самом деле, если задать замкнутый контур

в окрестности бесконечности, задать точку на контуре и следить за аргументом

при движении по контуру от заданной точки до неё же, то значение функции изменится на

. Т.е.

.
С другой же стороны, для

аналогичным образом при движении вокруг бесконечности эта функция сменит знак, т.е.

Следовательно, если

, то при движении по контуру вокруг бесконечности:

, откуда получаем, что

- точка ветвления.
Причиной вопроса был один сопливый момент: если

- точка ветвления для

,

- точка ветвления для

, то всегда ли для

точка

будет точкой ветвления?