Эх, хромает мой матанализ
На роль

просится

. Тогда оценка

(так вроде?) А это многовато.
То что стоит сейчас - получено полуинтуицией полуошибкой: забыл я интеграл нарисовать. Вышло
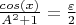
откуда

Эта оценка оказалась рабочей и живучей. Только препод хочет еще точнее и обоснованнее.
Он "хвост" от подобного интеграла как-то хитро взял по частям: у него увеличилась степень знаменателя, а следовательно и сходимость, а следовательно А можно выбрать меньше.