Я опять немного изменю терминологию. Пустую карточку буду называть
белой, а непустые
черными, причем различать черные карточки не имеет смысла. В начале игры (на «нулевом» ходу) была одна белая карточка, а затем после каждого хода в коробку либо добавлялась

черная карточка (если из коробки вынималась белая карточка), либо ничего не добавлялось (если из коробки вынималась черная). Значит, если после

ходов имеется

карточек, то белая карточка вынималась

раз, а черная

раз. Числа

и

для меня более удобны, и я буду ими пользоваться. Итак, ищется вероятность

того, что при заданном количестве ходов белая карточка вынималась

раз, а черная

раз.
Вероятность

равна сумме вероятностей всех различных взаимоисключающих вариантов-реализаций, при которых достигаются нужные

и

. Эти варианты отличаются порядком вынимания

белых и

черных карточек. Например, пусть

,

. Тогда последовательность может быть такой:

белая,

черных,

белая, –

белая,

черных,

белая,

черных.
В этом случае будем записывать:

. Эта краткая запись полностью описывает некоторую реализацию: из записи видно, что

(количество чисел), а

(сумма чисел), и каждое число означает количество черных карточек, вынутых после очередной белой. Ясно, что каждое число может принимать значения от

до

, но их сумма должна быть равна

– таковы ограничения.
Вероятность вынуть белую карточку равна

, а черную

, где

– текущее количество карточек, причем вначале

, а после каждой белой оно увеличивается. Выпишем вероятности, с которыми извлеченные карточки в нашем примере на каждом ходу имели именно такой цвет:

(белая),

(черная),

(черная),

(белая),

(белая),

(черная),

(черная),

(черная),

(белая),

(черная),

(черная),

(черная).
Вероятность данной реализации, т.е. последовательного осуществления этих событий, равна произведению выписанных чисел. После группировки "белых" множителей имеем

, где

, а их степени берутся последовательно из краткой записи

. Внимание

У

вверху индекс, у

-- степень.
В общем случае вероятность реализации

равна

.
Одну и ту же пару
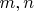
могут давать различные взаимоисключающие варианты-реализации, им соответствуют различные записи

с

числами, сумма которых равна

. Поэтому для нахождения

надо просуммировать выражения

для всевозможных комбинаций целых неотрицательных чисел

, сумма которых равна

.
Если

как общий множитель вынести за скобку, то в скобках останется как раз то, что называется
полный однородный симметрический многочлен степени

от

переменных

(
http://en.wikipedia.org/wiki/Complete_homogeneous_symmetric_polynomial, рекомендую начать с пункта Examples). Он обозначается

. Здесь мы попадаем в хорошо изученную область симметрических многочленов.
Итак,

, где

.
Пример. Найти вероятность получить после

-го хода

карточки.
Имеем:

,

. Общий факториальный множитель равен

.
Полином

-- это сумма всех

с целыми неотрицательными степенями

и

, сумма которых равна

. То есть

. Подставляя

,

, получим

.
Искомая вероятность

.
Итак, вопрос о явной формуле для вероятности сведен к вопросу о существовании явного выражения для полных однородных симметрических полиномов. Разработанность этой области дает некую уверенность в том, что формула существует...

Я также нарисовал красивую картинку, которая наглядно поясняет правила формирования вероятности одной реализации, но я не знаю, как ее вставить в сообщение.



