У Вас имеется набор чисел записанный в таблицу, в которой пронумерованы строки и столбцы. Каждый элемент в таблице это пересечение некоторой строчки и некоторого столбца, в частности, элемент

стоит на пересечении

-ой строчки и

-го столбца.
Каким образом, можно записать ограничение на сумму элементов

-го столбца? Используют обозначение

, то есть сумма элементов столбца

не превышает

.
Каким образом, можно записать ограничение на сумму элементов

-ой строки? Используют обозначение

, то есть сумма элементов строки

не превышает
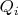
.
Каким образом, можно записать ограничение на сумму элементов таблицы? Используют обозначение

, то есть сумма элементов таблицы не превышает

.