dmd, у меня сначала тоже
возник такой вопрос, но потом я вспомнил, что есть такая формула (она легко выводится; предполагается, что

):

(не знаю, как она называется; аналогичная формула имеется и для комплексных чисел). С помощью этой формулы легко получается то выражение, которое нам продемонстрировал
Побережный Александр.
Три частных примера не являются доказательством.
Это контрпримеры к Вашему голословному утверждению, что в построенной Вами последовательности обязательно встретятся делители числа

.
Они могут содержать ошибки или быть исключениями из правила.
Если Вы утверждаете, что в моих вычислениях есть ошибка, то будьте любезны продемонстрировать нам правильные вычисления.
Исключениями они могут быть, но тогда Ваше правило должно быть сформулировано с явным указанием исключений и доказано для всех не исключительных

. Доказательство, кстати, обязательно должно присутствовать независимо от наличия исключений. Пока мы видим только голословные утверждения.
Если предполагать, что цепочка прямоугольников содержит прямоугольники с целыми сторонами, то рассмотрим новое число 2N и для этого числа применим рекурентную формулу, причем

.
Вы действительно верите, что, нагромождая квадратные корни, Вы, начав с

, на каком-то шаге
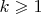
получите

? Приведите хотя бы один пример. И пусть даже получится не

, а хоть какое-нибудь целое число.