Асимптотические методы. Метод Лайтхилла.

[Palomnik]

Задача:
$(x + \xi\cdot y)\cdot y' + 6\cdot y' = 0$; с условием $y(1) = 1$
а) Построить прямое разложение второго порядка. Какова область неоднородности?
б) Построить разложение первого порядка (два члена по $ y $ и три члена по $ x $), используя метод Лайтхилла.


Мое решение:
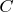
а) //В этой задаче я не совсем уверен верно ли я рассчитал коэффициент $ C $ для уравнений и правильно ли понял понятие 'второй порядок'
$(x + \xi\cdot y)\cdot y' + 6\cdot y' = 0$
Так как разложение второго порядка, то используем следующую формулу:
$y = y_0 + \xi\cdot y_1 + \xi^2\cdot y_2$
Подставляем второе уравнение в первое, раскрываем скобки и в итоге получаем:
$x\cdot y_0' + \xi\cdot y_0\cdot y_0' + \xi^2\cdot y_1\cdot y_0' + \xi^3\cdot y_2\cdot y_0' + \xi\cdot x\cdot y_1' + \xi^2\cdot y_0\cdot y_1' + \xi^3\cdot y_1\cdot y_1' + \xi^4\cdot y_2\cdot y_1' + \xi^2\cdot x\cdot y_2' + \xi^3\cdot y_0\cdot y_2' + \xi^4\cdot y_1\cdot y_2' + \xi^5\cdot y_2\cdot y_2' + 6\cdot y_0 + 6\cdot\xi\cdot y_1 + 6\cdot\xi^2\cdot y_2= 0$

Выписываем множители при эпсилон и решаем дифференциальные уравнения:
$\xi^0 : x\cdot y_0' + 6\cdot y_0 = 0$
$\xi^1 : x\cdot y_1' + y_0\cdot y_0' + 6\cdot y_1 = 0$
$\xi^2 : x\cdot y_2' + y_0\cdot y_1' + y_1\cdot y_0' + 6\cdot y_2 = 0$

Из первого уравнения получаем:
$y_0 = x^{-6}\cdot C$, где, подставляя начальное условие $y(1) = 1$, получим, что $ C = 1$, а значит решение будет выглядеть так: $y_0 = x^{-6}$

Аналогично получаем из второго уравнения:
$y_1 = x^{-6}\cdot C - \frac{6}{7\cdot x^{13}}$, где, подставляя начальное условие $y(1) = 1$, получим, что $ C = \frac{13}{7}$, а значит решение будет выглядеть так: $y_1 = \frac{13}{7\cdot x^6} - \frac{6}{7\cdot x^{13}}$

Так же получаем из третьего уравнения:
$y_2 = x^{-6}\cdot C - \frac{6\cdot (26\cdot x^7 - 9)}{49\cdot x^{20}}$, где, подставляя начальное условие $y(1) = 1$, получим, что $ C = \frac{151}{49}$, а значит решение будет выглядеть так: $y_1 = \frac{151}{49\cdot x^6} - \frac{6\cdot (26\cdot x^7 - 9)}{49\cdot x^{20}}$

Затем полученное решение для $y_2$, $y_1$ и $y_0$ подставляем в уравнение: $y = y_0 + \xi\cdot y_1 + \xi^2\cdot y_2$ и получаем ответ для пункта а) этой задачи:

$y = x^{-6} + \xi\cdot (\frac{13}{7\cdot x^6} - \frac{6}{7\cdot x^{13}}) + \xi^2\cdot (\frac{151}{49\cdot x^6} - \frac{6\cdot (26\cdot x^7 - 9)}{49\cdot x^{20}}) + O(\xi^3)$

А в точке $x = 0$, функция будет неоднородна.

б)
Чтобы разобраться в этом методе ознакомился с книгой "Методы возмущений" Найфэ А.Х.. Там на страницах 93-96 идет разбор примера несколько похожим на мой, однако, я не могу согласовать требование указанное в скобках: "два члена по $ y $ и три члена по $ x $" и приводимый там пример. Не могли бы вы мне помочь с методом решения этой задачи (возможно, подсказать какую-нибудь другую литературу по этому вопросу с более приближенными к моей задаче примерами)

[V.V.]

А почему для поправок Вы берете $y_1(1)=1$ и $y_2(1)=1$? Ведь тогда получается $y(1)=1+\xi+\xi^2$. На самом деле, там $y_1(1)=0$ и $y_2(1)=0$.

Для второй задачи надо разлагать не только $y$ по степеням $\xi$, но и сделать замену независимой переменной $x=t(1+h_1\xi+h_2\xi+\ldots)$.

[Palomnik]

Спасибо за советы.

- Что касается определений условий, понял свою ошибку, исправлю. Только вот, я не уверен я правильно истолковал "второй порядок" и не стоит ограничится уравнением $y = y_0 + \xi\cdot y_1$ вместо $y = y_0 + \xi\cdot y_1 + \xi^2\cdot y_2$ ?

- Не совсем ясна ваша подсказка. В рассмотренном примере у Найфэ по степеням $\xi$ разлагается только некоторая величина $ s $ и я не совсем понял, во-первых, что даст разложение $x = t\cdot (1 + h_1\cdot\xi + h_2\cdot\xi + ...)$, а во-вторых, о каком разложении $ y $ по степеням $\xi$ идет речь.
Не могли бы вы привести конкретный пример или показать краткое схематичное решение этого примера?

[V.V.]

Palomnik в сообщении #265414 писал(а):

и я не совсем понял, во-первых, что даст разложение $x = t\cdot (1 + h_1\cdot\xi + h_2\cdot\xi + ...)$

Допустим у нас есть система, и мы хотим найти её периодическое решение. Пусть при $\xi$ система периодическое решение имеет, а возмущение аналитическое от $\xi$. Но при таком возмущении все характеристики системы будут аналитическими по $\xi$, в том числе, период движения по замкнутой кривой. И в такой задаче замена переменной очень естественна.

[V.V.]

Пример.

Рассмотрим уравнение ван дер Поля с малым параметром $\mu$:
$\ddot{x}+x=\mu \dot{x}(1-x^2)$.

Можно показать, что интересующее нас уравнение имеет предельный цикл; его амплитуда и период - аналитические функции $\mu$.

Так как период - аналитическая функция $\mu$, сделаем замену переменной:
$\tau=t(1+h_1\mu+h_2\mu^2+\ldots)$.

Тогда $\frac{dx}{dt}=\frac{dx}{d\tau}(1+h_1\mu+h_2\mu^2+\ldots)$, $\frac{d^2x}{dt^2}=\frac{dx}{d\tau}(1+h_1\mu+h_2\mu^2+\ldots)^2$.

Решение также будем искать в виде ряда: $x=x_0+\mu x_1+\mu^2 x_2+\ldots$.

Подставляя наши разложения в уравнения и беря коэффициенты при $\mu^0$, $\mu^1$, $\mu^2$, получаем
$x_0''+x_0=0$ (штрихом обозначаем проиводную по $\tau$),
$x_1''+x_1=-2h_1x_0''+x_0'(1-x_0^2)$,
$x_2''+x_2=-2h_1x_1''-(2h_2+h_1^2)x_0''+(h_1x_0'+x_1')(1-x_0^2)-2x_0'x_0x_1$.

Ищем $x_0$, $x_1$, $x_2$ как периодические функции с периодом $2\pi$. Без ограничения общности можем считать, что $x_0(0)=a$, $x_i'(0)=0$, $i\geqslant 0$.

Тогда $x_0=a\cos\tau$.

Подставляем $x_0$ в уравнение для $x_1$. Имеем
$x_1''+x_1=2h_1a\cos\tau-a\sin\tau+a^3 (\sin 3\tau+\sin\tau)/4$.
Для того, чтобы было периодическое решение с периодом $2\pi$ необходимо отсутствие резонансных слагаемых в правой части.
При $\sin\tau$ коэффициент $a^3/4-a$, при $\cos\tau$ коэффициент $2h_1a$.

Рассмотрим $a=2$ (никто не мешает взять и $-2$, но мы все равно попадем на тот же предельный цикл, только начальная точка будет другой). Тогда $h_1=0$.

Решаем уравнение на $x_1$, получаем
$x_1=A_1\cos\tau+B_1\sin\tau-\frac{1}{4}\sin 3\tau$.

И условия $x_1'(0)=0$ получаем, что $B_1=3/4$. Из условия отсутствия резонансный слагаемых в уравнении на $x_2$ получим, что $A_1=0$, $h_2=-1/16$.

В итоге получаем асимптотику
$x=2\cos\tau+\frac{\mu}{4}(3\sin\tau-\sin 3\tau)+{\cal O}(\mu^2)$, где
$\tau=t\left(1-\frac{\mu^2}{16}+{\cal O}(\mu^3)\right)$.

О! В этом примере как раз два члена разложения по $x$ и три по $t$.

[Stupid]

А как найти равномерное приближение к решению уравнения, используя метод Лайтхилла? Разложения какого порядка находить?