Читаю один курс лекций по АГ, там дается в качестве упражнения вариант леммы Йонеда, и тут как раз вопрос.
Цитата:
Suppose

is an object of category
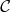
. For any object
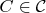
, we have a set of morphisms
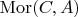
. If we have a morphism
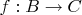
, we get a map of sets
(2)
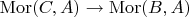
by composition: given a map from

to

, we get a map from

to

by precomposing with

. Hence this gives a contravariant functor
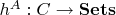
. Yoneda's Lemma states that the functor
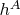
determines

up to unique isomorphism. More precisely:
Given two objects

and

, and bijections
(3)
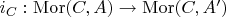
that commute with the maps (2), then the
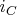
must be induced from a unique isomorphism
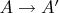
.
а) Что же в данном случае означает "commutes"? От обычного смысла как-то тепло не делается.
б) И как же в таком случае доказывать?
(Сначала так или иначе подставляем

в
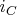
и смотрим, что происходит с
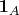
, образ этого морфизма и должен бы быть исходным изоморфизмом. Но при проверке того, что это изоморфизм, видимо, надо как-то воспользоваться этим самым "commutes", с чем проблема)