Это краткое сообщение, являющееся результатом странной
сделки с
cepeshe'ем (админ-ом) и написанное в стиле copy-paste на основе информации из различных источников, адресовано участникам форума dxdy и посвящено краткому описанию работы с пакетом
. Здесь приведены общие сведения о пакете, рассказано о некоторых из его возможностей, а также дано описание способов его использования на данном ресурсе.
Напомню, что на форуме dxdy, учитывая сдвиг целевой аудитории в математическую сторону, функционирует мощная система отображения формул, основанная на

Д.Кнута; а для облегчения верстки используется макропакет

с некоторыми дополнительными полезными
пакетами, одним из которых является пакет
, написанный специально для рисования диаграмм со структурой графа (т.е. преимуществено для прорисовки простых графических объектов и, что самое главное, связей между ними).
Рассматриваемый пакет поддерживает несколько способов, или лучше сказать, стилей набора диаграмм, а в основе лежит простой (хотя, на первый взгляд, достаточно запутанный) язык с обилием мнемонических кострукций. Например, аналог стрелки

может быть нарисован с использованием этого пакета под любым углом, любой длины, любой формы; при этом стиль такой стрелки при наборе диаграммы схематически обозначается тройкой символов
|->, сплошная линия обозначается символом
-, а для прорисовки пунктирной линии используется пара
--, ну и т.д.
Причем, в отличие от базовых графических возможностей

'а, пакет
нацелен на более гибкую, логическую разметку диаграмм; так например, достаточно указать, что некоторый объект должен быть соединен с другим объектом стрелкой такого-то стиля, детали же прорисовки будут уточняться уже самим макропакетом. Конечно, в реальности все не так идеально и жесткой привязки к конкретным координатам и размерам порой избежать не удастся, но общая философия
'а способствует использованию более удобного относительного позиционирования объектов (а ведь по названию и не скажешь). Сверх того, возможность и неизбежность использования координат на самом деле должны расцениваться как одно из главных достоинств описываемого пакета, обеспечивающее при необходимости высокую точность построений.
Пакет
особенно популярен при наборе простых графов и теор-категориальных коммутативных диаграмм. Поэтому наш краткий обзор начнется с рассмотрения именно этих конструкций, поддержка которых осуществляется расширением
matrix.
Команда
\xymatrix{...} создает прямоугольную таблицу-матрицу, в ячейках которой могут быть размещены любые визуальные объекты; использование этой команды похоже на применение привычных табличных окружений вроде
tabular. Например, код
\xymatrix{A&B&C\\D&&{\bullet}} приводит к отображению следующей диаграммы:

Здесь ячейки в строке как всегда разделяются символом
&, а сами строки -- командой перевода строки, например
\\. Важно запомнить, что содержимое ячейки не может начинаться с какой-либо макрокоманды, именно поэтому в приведенном выше примере использовалась дополнительная пара фигурных скобок вокруг команды
\bullet.
Для оформления ячеек предусмотрены специальные конструкции-модификаторы. К примеру, можно сделать нечто подобное:
![$$\xymatrix{
A & *+[F]{B} & C \\
*+[o]+[F]{D} & & {\bullet}
}$$ $$\xymatrix{
A & *+[F]{B} & C \\
*+[o]+[F]{D} & & {\bullet}
}$$](https://dxdy-04.korotkov.co.uk/f/3/f/0/3f034f6a88cbc4432d9b96211a64185982.png)
Это достигается использованием следующего кода:
\xymatrix{
A & *+[F]{B} & C \\
*+[o]+[F]{D} & & {\bullet}
}
Но основная же мощь заключается в рисовании соединений, т.е. стрелок между объектами. Вообще, рисовать стрелки -- это пожалуй лучшее, что умеет делать
.
В каждой ячейке матрицы, непосредственно после содержимого ячейки, могут располагаться команды построения стрелок
\ar. Каждая такая команда рисует стрелку, направленную от объекта в текущей ячейке к некоторому другому объекту, возможно тоже лежащему в одной из ячеек. При использовании команды
\ar необходимо указать некоторые параметры, особенно направление стрелки, для задания которого в квадратных скобках после команды указывается последовательность символов из набора
u,
d,
r,
l, служащих для обозначения направлений вверх, вниз, вправо и влево, соответственно (причем для продления стрелки каждое направление может указываться многократно); а если оставить квадратные скобки пустыми, то стрелка будет идти от текущей ячейки к ней же самой (важно заметить, что на самом деле в пакете
есть и другие способы задания направлений и позиций). Например, команда
\ar[drr], набранная в верхней-левой ячейке матрицы создаст стрелку, направленную на нижнюю-правую ячейку (один раз смещаемся вниз и дважды вправо, прямо по указанной последовательности
drr):
![$$\xymatrix{
A \ar[drr] & *+[F]{B} & C \\
*+[o]+[F]{D} & & {\bullet}
}$$ $$\xymatrix{
A \ar[drr] & *+[F]{B} & C \\
*+[o]+[F]{D} & & {\bullet}
}$$](https://dxdy-02.korotkov.co.uk/f/5/4/e/54ec8d15fbb4d130b27f22a173635a6282.png)
На всякий случай приведу исходный код:
\xymatrix{
A \ar[drr] & *+[F]{B} & C \\
*+[o]+[F]{D} & & {\bullet}
}
Для смены стиля стрелки испольуется конструкция-модификатор
@{...}, вставляемая между
\ar и указывающими направление стрелки квадратными скобками. На месте многоточия может быть последовательность символов, обозначающая стиль стрелки. Некоторые из возможных стилей уже были рассмотрены (
|->,
- и
--), но может быть использовано множество других, например
.,
~,
~~,
),
^(->, и т.д. Кроме того, между
@ и открывающей фигурной скобкой могут располагаться дополнительные символы,
^ или
_, а также числа от 0 до 3, управляющие чем-то вроде параллельного смещения, а также кратностью стрелок. Приведу парочку образцов:

Среди прочего, имеется возможность нарисовать стрелку не только напрямую соединяющую два объекта, но и по-пути проходящую через ряд других ячеек таблицы.
Для этого необходимо в коде перед набором каждого промежуточного сегмента стрелки вставлять символ
' (апостроф). Заметьте, что направление на каждый следующий узел указывается относительно начальной ячейки для этой стрелки, а не относительно текущего узла на её пути. Кстати, отдельные сегменты такой ломаной стрелки в некотором смысле независимы и могут оформляться отдельно.
Сказанного уже достаточно для верстки примерно такой вот красотищи:
![$$\xymatrix@!0{
& \lambda \omega \ar@{-}[rr] \ar@{-}'[d][dd]
&& \lambda C \ar@{-}[dd]
\\
\lambda 2 \ar@{-}[ur] \ar@{-}[rr] \ar@{-}[dd]
&& \lambda P2 \ar@{-}[ur]\ar@{-}[dd]
\\
& \lambda \underline\omega \ar@{-}'[r][rr]
&& \lambda P \underline\omega
\\
\lambda{\to} \ar@{-}[rr] \ar@{-}[ur]
&& \lambda P \ar@{-}[ur]
}$$ $$\xymatrix@!0{
& \lambda \omega \ar@{-}[rr] \ar@{-}'[d][dd]
&& \lambda C \ar@{-}[dd]
\\
\lambda 2 \ar@{-}[ur] \ar@{-}[rr] \ar@{-}[dd]
&& \lambda P2 \ar@{-}[ur]\ar@{-}[dd]
\\
& \lambda \underline\omega \ar@{-}'[r][rr]
&& \lambda P \underline\omega
\\
\lambda{\to} \ar@{-}[rr] \ar@{-}[ur]
&& \lambda P \ar@{-}[ur]
}$$](https://dxdy-03.korotkov.co.uk/f/a/2/a/a2a5a660d61b5c3682be9f762168acb282.png)
Исходный код этого лямбда-куба:
\xymatrix@!0{
& \lambda \omega \ar@{-}[rr] \ar@{-}'[d][dd]
&& \lambda C \ar@{-}[dd]
\\
\lambda 2 \ar@{-}[ur] \ar@{-}[rr] \ar@{-}[dd]
&& \lambda P2 \ar@{-}[ur]\ar@{-}[dd]
\\
& \lambda \underline\omega \ar@{-}'[r][rr]
&& \lambda P \underline\omega
\\
\lambda{\to} \ar@{-}[rr] \ar@{-}[ur]
&& \lambda P \ar@{-}[ur]
}
Здесь используется указание стиля стрелки (сплошная линия без "наконечника") и вышеописанный прием с рисованием многосегментных стрелок (разрывы между сегментами используются для схематичного обозначения соединений, более удаленных от наблюдателя).
Стрелки можно снабжать надписями, над и под стрелкой, используя символы
^ и
_, как при обычном наборе верхних и нижних индексов, например
\ar[r]^{a}_{b} (если необходимо вывести надпись прямо посередине стрелки, то непосредственно после символа
^ или
_ следует вставить символ
-); а можно разместить надпись прямо в разрыве стрелки действуя по той же схеме, но используя символ
| (разрыв можно оставить пустым, разместив в нем вместо надписи команду
\hole). Пример (коммутативная диаграмма поднятия

непрерывной функции

):
![$$\xymatrix{
\mathbb{X} \ar[r]^-F \ar[d]^-\pi & \mathbb{X} \ar[d]^-\pi \\
\mathbb{Y} \ar[r]^-f & \mathbb{Y}
}$$ $$\xymatrix{
\mathbb{X} \ar[r]^-F \ar[d]^-\pi & \mathbb{X} \ar[d]^-\pi \\
\mathbb{Y} \ar[r]^-f & \mathbb{Y}
}$$](https://dxdy-01.korotkov.co.uk/f/8/2/0/8202a38dba534e9b2f3fab67eecb10bd82.png)
Исходный код этого примера:
\xymatrix{
\mathbb{X} \ar[r]^-F \ar[d]^-\pi & \mathbb{X} \ar[d]^-\pi \\
\mathbb{Y} \ar[r]^-f & \mathbb{Y}
}
Непосредсвенное перед надписью могут быть добавлены спецификаторы, указывающие явное положение метки относительно стрелки. Один из таких спецификаторов наиболее интересен. Он имеет форму
!{a;b}, где
a и
b -- направления (набранные с использованием уже знакомых последовательностей в квадратных скобках) на некоторые две ячейки. Такой спецификатор позволяет разместить надпись в месте пересечения текущей стрелки и стрелки, соединяющей указанные ячейки. С использованием этого приема ранее сверстанный лямбда-куб может быть набран так:
\xymatrix@!0{
& \lambda \omega \ar@{-}[rr] \ar@{-}[dd]|!{[dl];[dr]}\hole
&& \lambda C \ar@{-}[dd]
\\
\lambda 2 \ar@{-}[ur] \ar@{-}[rr] \ar@{-}[dd]
&& \lambda P2 \ar@{-}[ur]\ar@{-}[dd]
\\
& \lambda \underline\omega \ar@{-}[rr]|!{[ur];[dr]}\hole
&& \lambda P \underline\omega
\\
\lambda{\to} \ar@{-}[rr] \ar@{-}[ur]
&& \lambda P \ar@{-}[ur]
}
К сожалению, эта безусловно полезная возможность не работает для изогнутых стрелок.
Кстати, да,
поддерживает не только прямые стрелки. Действительно, часто, особенно при рисовании графов, конечных автоматов и пр., изогнутые стрелки оказываются просто необходимы. Для набора изогнутых стрелок нужно использовать конструкцию
@/.../, например вставив её после
\ar. На месте многоточия может быть символ
^ или
_ для верстки стрелок обращенных выпуклостью "вверх" или "вниз", соответственно (если воспринимать стрелку направленной "горизонтально" и "вправо"). Между этим символом и закрывающей косой "скобкой" может быть также указана степень выпуклости (в виде размерной величины, например
1pc). Замечательно то, что стрелки могут быть изогнуты более сложным образом, для чего применяется конструкция
@(a, b), где
a и
b -- направления исхода стрелки из начальной ячейки и входа её в конечную. Можно использовать следующие направления:
u,
ur,
r,
dr,
d,
dl,
l и
ul, смысл которых, думаю, понятен без дополнительных пояснений. Пример:
![$$\xymatrix{
A \ar@(ur,dl)@{-}[dr] & B \ar@/^/@{--}[dl] \\
C & D
}$$ $$\xymatrix{
A \ar@(ur,dl)@{-}[dr] & B \ar@/^/@{--}[dl] \\
C & D
}$$](https://dxdy-04.korotkov.co.uk/f/f/d/b/fdbd65457fcfa27d3d4af141bfb94fda82.png)
Его исходный код:
\xymatrix{
A \ar@(ur,dl)@{-}[dr] & B \ar@/^/@{--}[dl] \\
C & D
}
При рисовании стрелки можно "на лету" модифицировать её объект назначения (тот, на которой она указывает). Наиболее полезной является возможность изменять положение такого объекта, что достигается использованием мидификатора
!. После восклицательного знака необходимо указать направление смещения. Ранее уже были рассмотрены возможные буквосочетания, применяемые для спецификации направлений, но в данном случае символы должны быть прописными (в верхнем регистре). Этот прием часто используют для размещения надписей к объектам. Пример:
![$$\xymatrix{
A \ar@{--}[rrd]*++!LD{p} & B & C \\
D & E & {\bullet}
}$$ $$\xymatrix{
A \ar@{--}[rrd]*++!LD{p} & B & C \\
D & E & {\bullet}
}$$](https://dxdy-01.korotkov.co.uk/f/0/9/6/096410f01bc3532f2f6ae3eb2996ac7a82.png)
А код выглядит так:
\xymatrix{
A \ar@{--}[rrd]*++!LD{p} & B & C \\
D & E & {\bullet}
}
Плюсики здесь используются для увеличения промежутка между объектом и надписью -- чем больше плюсиков, тем больше промежуток.
Благодаря опции
poly объекты могут размещаться не только в узлах прямоугольной сетки, но и в вершинах многоугольников. Для верстки многоугольника используется команда
\xypolygon, непосредственно после которой указывается число сторон (большее двух разумеется), а затем в фигурных скобках указывается либо объект, размещаемый на месте вершин многоугольника, либо более сложная конструкция (последовательность спецификаторов), контролирующая кроме прочего способ соединения (тип линий, возможно с разрывами и надписями) вершин друг с другом и с центром многоугольника. В качестве спецификаторов могут использоваться такие строчки как
~:{...}, использующаяся для масштабирования;
~*{...} для размещения объектов в вершинах;
~<{...} или
~<<{...} для управления соединениями вершин с центром;
~<>{...} для размещения разрывов и меток на этих соединениях;
~>{...} для управления стилем прорисовки сторон многоугольника; и др.
Вершинам многоугольника автоматически присваиваются имена путем нумерации с единицы. Кроме того, перед открывающей фигурной скобкой, но после числа сторон, может быть указан в двойных кавычках префикс, добавляемый к имени каждой вершины для удобства её адресации.
Примеры:
\begin{xy}/r2pc/:
{\xypolygon6{\bullet}},
+/r5pc/, {\xypolygon6{~*{\bullet}~><{}}},
+/r5pc/, {\xypolygon6{~<<{@{->}}~>{{--}}}}
\end{xy}
Этот код строит следующее изображение:

Многоугольники также пригодны для верстки таких вот пирамидок:

Исходник:
\begin{xy}/r2pc/:
="a", +(.2,1.5)="b", "a",
{\xypolygon5{~:{(1,-.1):(0,.33)::}~<>{;"b"**@{-}}}},
(5,0)="0", +(-0.8,3)="T","0",
{\xypolygon6{~:{(1,0.2):(0,.4)::}~<>{;"T"**@{-}}}}
\end{xy}
В последних примерах можно заметить некоторые странности не вписывающиеся в намеченную схему. Дело в том, что, фактически, команды вроде
\xymatrix или
\xypolygon являются всего-лишь обертками над несколько более низкоуровневым языком
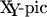
. Выражение "интуитивно-понятный" можно применять к чему угодно, но только не к этой вещи. Хотя в основе лежит очень простая последовательность действий: выбор расположения объектов, размещение объектов в выбранных позициях, соединение объектов "линиями".
Команды можно набирать, используя окружение
xy и соответствующие примеры использования такого окружения уже были приведены. Поэтому сейчас сосредоточимся на приемах верстки объектов и соединений. Итак, при верстке объекта сначала указывают его положение, например в декартовых координатах, используя для этого нотацию с круглыми скобками, вроде
(x,y). Общий же вид необходимой нам конструкции таков:
(x,y)*{...}, где на месте многоточия как раз таки и размещается нужный объект. Для набора соединителя используется конструкция
**{...} (на деле, используется что-то вроде
**\dir{...} или
**@{...}). Так для набора следующей диаграммы

применялся такой код:
\begin{xy}
(0,0)*{A};
(20,0)*{B};
**@{-}
\end{xy}
NB, здесь команда прорисовки соединителя использует позиции "текущего" (только что набранного) и "предыдущего" объектов; вообще, в
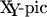
эта концепция встречается сплошь и рядом.
Код можно немного усовершенствовать:
\begin{xy}
(0,0)*+{A}="A";
(20,0)*+{B}="B";
{\ar@{->} "A";"B"}
\end{xy}
Это даст такой результат:

Здесь вы можете видеть уже знакомый по примеру с пирамидами прием с присваиванием строковых идентификаторов к объектам и использованием этих идентификаторов в дальнейшем вместо явных координат.