Первый деньProblem 1. Let

Prove that
 Problem 2.
Problem 2.Compute the sum of the series
 Problem 3.
Problem 3. Define the sequence

inductively by

and

for each

Compute
 Problem 4.
Problem 4. Let

be two integers and suppose that

is a positive integer for which the set

is finite.
Prove that
 Problem 5.
Problem 5. Suppose that

are real numbers in the interval
![$[-1,1]$ $[-1,1]$](https://dxdy-03.korotkov.co.uk/f/6/9/9/699628c77c65481a123e3649944c0d5182.png)
such that

Prove that

for all positive integers
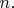
Duration is probably 5 hours and each problem is given 10 points.
Второй деньProblem 1. 
A sequence

of real numbers satisfies

Does it follows that this sequence converges for all initial values

(5 points)

A sequence

of real numbers satisfies

Does it follows that this sequence converges for all initial values

(5 points)
Problem 2. Let

be positive real numbers such that

for all

Prove that

(10 points)
Problem 3. Denote by
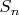
the group of permutations of the sequence

Suppose that

is a subgroup of

such that for every

there exists a unique

for which

(Here

is the unit element of the group

) Show that this

is the same for all

(10 points)
Problem 4. Let

be a symmetric

matrix over the two-element field all of whose diagonal entries are zero. Prove that for every positive integer

each column of the matrix

has a zero entry.(10 points)
Problem 5. Suppose that for a function
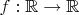
and real numbers

one has

for all

Prove that

for all

if

for every prime number

and every real number

(10 points)
Duration: 5 hours
(имхо)
Минимум пять задач (в первый день: 1,2,3,5 и во второй день: 2) доступны средним школьникам. Всё это выглядит как розыгрыш, но вроде бы именно эти задачи и были.



