Есть процесс Орнштейна-Уленбека:

. И есть его дискретное представление, приведенное во всех источниках, при

:

. Я не могу понять, что с первыми слагаемыми: насколько я понимаю, используется эквивалентность функций. Но при
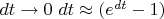
, то есть

Что я делаю не так? Здесь не может применяться такой предельный переход? А тогда каким образом происходит дискретизация? Спасибо!