Добрый день,
я хотел бы для простой последовательности

,

найти
1.

; 2.

3.

; 4.

.
Проверьте, пожалуйста, верно ли я рассуждаю:
Определения:1.


a)

, для

b) для




.
2.


a)

, для

b) для




.
3.

4.
 Решение (пока только первые 2 пункта):
Решение (пока только первые 2 пункта):0. Когда мы говорим об

мы имеем ввиду инфимум
значений последовательности:

- верно? (также и с

).
1.

, т.к.:
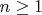



, и значит

- нижняя граница последовательности.
Теперь пусть дано

, тогда должен существовать такой номер

, что

Это неравенство выполняется при всех

. Тогда я могу положить

для любого

, и

- верно?
2.

, т.к.:
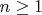



, и значит

- верхняя граница последовательности.
Теперь пусть дано

, тогда должен существовать такой номер

, что

, как только

. Это неравенство выполняется при всех

. Тогда

, и

- верно?
Спасибо!