Геометрическая задача

[Ranax]

Вспомнилась одна задачка любителя геометрии.Дан квадрат$ABCD$, через середину квадрата проходит прямая, и на этой прямой взята точка$O$ так, что угол$AOD$ равнялся $75$ градусам.Найти угол$BOC$
P.S. Задача имеет красивое и короткое решение

[ИСН]

В условии чего-то не хватает.

[Ranax]

чего?

[maikle]

Не хватает того, где именно расположена точка О.

[Ranax]

она расположена на прямой, проходящей через центр квадрата(не по диагонали) и распол так, что угол$AOD$ равнялся $75$ гр

[ИСН]

Все точки плоскости расположены на прямых, проходящих через центр квадрата. Чем выделяется эта?

[Ranax]

эта прямая проходит через середины сторон $BC$ и $AD$, точка $O$ расположена на этой прямой, внутри квадрата
понятно?

[ИСН]

Вот теперь совсем другое дело.

[dilyara-94]

Не совсем поняла, почему "совсем другое дело". Эта точка будет единственной, которая удовлетворяет условию задачи?

[Ranax]

ну да

[VoloCh]

Пусть $2\alpha=75^\circ$. Тогда искомый угол равен $2\arctg\left(\dfrac{\tg\alpha}{2\tg\alpha-1}\right)$, но это "плохой" угол. Решение "короткое", но не "красивое".

[Ranax]

угол будет целочисленным

-- Пт июн 18, 2010 18:39:52 --

эх, полный штиль

[Батороев]

Штиль оттого, что решение VoloCh верное и добавить нечего.

[VoloCh]

Значит, я (мы) не понял(и) условия. Итак есть, квадрат $ABCD$ (для простоты со стороной, равной 2), точки $G$ и $F$ соответственно середины $BC$ и $AD$. Тогда $\angle AOF=\alpha=\dfrac{75^\circ}2$, аналогично , $\angle BOG=\beta=\dfrac{\angle BOC}2$. Далее, так как $O$ внутри квадрата по уточнению, то $FO+OG=\ctg\alpha+\ctg\beta=2$. Отсюда мой нецелый ответ. Где ошибка?

[age]

Ranax в сообщении #332454 писал(а):

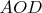
Вспомнилась одна задачка любителя геометрии.Дан квадрат$ABCD$, через середину квадрата проходит прямая, и на этой прямой взята точка$O$ так, что угол$AOD$ равнялся $75$ градусам.Найти угол$BOC$
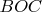
P.S. Задача имеет красивое и короткое решение

Ну во-первых, начнем с того, что г.м.точек, образующих с двумя данными угол $75^\circ$ есть эллипс, малой полуосью которого является сторона $AD$ квадрата. Таким образом, на каждой прямой, проходящей через центра квадрата и не пересекающей сторону $AD$, есть ровно две точки, угол с которыми равен $75^\circ$. На прямой, пересекающей сторону $AD$, - ровно одна точка.
Но геометрическим местом точек, образующих некоторый одинаковый угол $\alpha$ со стороной $BC$ будет также некоторый эллипс.
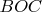
Таким образом, будет лишь две точки с одинаковыми углами $BOC$ - точки пересечения эллипсов.
Но для каждой такой точки будет только одна прямая, проходящая через центр квадрата.
Таким образом, таких прямых бесконечное множество.