Ага, кажется дошло. Оказывается
iig имел ввиду раскраску граней графа, двойственного графу смежности стран! То есть речь идет о раскраске именно
контурной политической карты. Так в примере
Xaositect'а действительно есть одна нечетная вершина на пересечении границ, поэтому его грани не 2-раскрашиваемы. :) А если все вершины четные, то вот тогда грани такого графа и можно будет раскрасить всего двумя цветами. В рекомендованной
iig'ом книжке это утверждение доказывается по индукции примерно так. Сначала выводится, что в рассматриваемом графе через любую вершину можно провести простой цикл. Итак, допустим, что вершину и цикл выбрали. Теперь этот цикл аккуратно удаляется, а оставшийся граф пофасеточно раскрашивается двумя красками (рекурсивно). После этого удаленный цикл можно восстановить и просто инвертировав цвета граней, им ограниченных, немедленно получить искомый граф с 2-раскрашенными гранями.
Ok, с этим ясно. Но как быть с нечетными вершинами? Пытаться склеить их в одну особую вершину с четной степенью? И что делать с оставшимися бесцветными странами? В общем, я опять запутался... :)
Кстати, думаю не лишним будет упомянуть ещё парочку известных мне простых наивных доказательств 4CT.
Вот например, некий I.Cahit строит спиральки на графах и успешно их (графы) раскрашивает (
arXiv:math/0408247). То есть, он описывает алгоритмы раскраски и пытается показать их правильность, корректность, и т.д. Уровень строгости доказательств какое-то недоверие вызывает, хотя, я, честно говоря, все равно мало чего из его писанины понял. :) Да и вообще странный он какой-то, к примеру, судя по некоторым высказываниям, он не подозревает о необобщаемости 4CT на высшие размерности... :)
Есть ещё один чудик, некий Fayez A.Alhargan, так он вообще 4CT буквально в одну строку "решил". Пожалуй попробую кратко пересказать ход его мыслей.
Сначала он показывает, что если граф содержит подграф, изоморфный

с
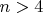
, то все, приехали, четырьмя красками не обойтись (в принципе, это очевидно). Затем пытается доказать, что у планарного графа нет и быть не может такого слишком большого полного подграфа.
Делает он это примерно так. Пусть у графа есть

вершин,

ребер и

граней. Fayez замечает, что каждая страна на проблемной карте имеет как минимум три соседа, т.е., у каждой грани графа контурной карты (дуального графу соседства) имеется как минимум
три ребра, что с учетом соответствия каждого ребра куску границы между максимум
двумя странами приводит к неравенству

, которое вместе с формулой Эйлера

дает ещё одно неравенство

(это известный результат для планарных графов, популярное изложение см. например в А.Ю.Ольшанский, Плоские графы, СОЖ, №11, 96г.).
Теперь Fayez подставляет в это неравенство значение

для полного графа, которое может быть получено из комбинаторных соображений; именно, для

число

(количество ребер) равно

, т.е., количеству единиц над главной диагональю

матрицы забитой единицами. Подстановка в ранее полученную формулу дает квадратное неравенство

, которое имеет решение
![$n\in[3;\ 4]$ $n\in[3;\ 4]$](https://dxdy-04.korotkov.co.uk/f/3/4/7/347d0289472aa6325a062d56a3e8e99a82.png)
. Из этого результата сразу же и делается вывод о несуществовании у планарного графа более чем 4-вершинного полного подграфа (точнее говоря, вывод о неукладываемости

, что почти тоже самое). :)
Хм, неужели действительно из последнего вывода следует 4-раскрашиваемость карты? Интуитивно, да, если потребовалась пятая краска при оптимальном раскрашивании полит. карты, значит текущая страна граничит с четырьмя другими, на которые уже растрачена 4-палитра, т.е, с четырьмя странами, граф соседсва для которых полный. Но ведь это не исключает существования какого-нибудь иного сценария неэкономичного использования красок... В общем, мне почему-то кажется, что здесь есть какая-то логическая проблема (типа импликации в одну сторону вместо эквивалентности)... Иначе, какого [вырезано] вокруг 4CT было столько шумихи и горы сгенерированной компьютером макулатуры? :)
Честно говоря, когда-то я тоже пытался одолеть 4CT быстро и просто. Целых две недели мозги ломал. Но стоит ли говорить, что ничего дельного так и не придумал? :) Тем не менее, если вспомню, что именно я тогда накуралесил, то, наверное, напишу сюда... Но мой подход, мягко говоря, сильно отличался от рассуждений
iig'а.



