Теория вероятностей

[ant]

Проверьте, пожалуйста, правильность решения задач:
1) Выбраны два числа $m$ и $n$, причём $0<m \le 3$, $0<n \le 3$. Найти вероятность того, что $m$ и $n$ такие, что $mn \le 2$ и $\frac m n \le 3$
Решение: Получается, что $m \le \frac 2 n$ и $m \le 3n$
Строим график:

Вычисляем площадь заштрихованной фигуры:

$$\int_{0}^{\sqrt {\frac 2 3}} 3n dn+\int_{\sqrt {\frac 2 3}}^{3} \frac 2 n dn=3.603$$

Искомая вероятность: $P=\frac {3.603} {9}=0.4$
2) Трое бросают монету до выпадения орла, что считается выйгрышем. Определить, как соотносятся вероятности выйгрыша второго и третьего.
Решение: Благоприятные варианты исхода для второго игрока (о - орёл, р - решка):
р,о
р,р,р,р,о и т.д
Для третьего:
р,р,о
р,р,р,р,р,о и т.д.
Вероятность выйгрыша второго игрока: $P(A)=(\frac 1 2)^2+(\frac 1 2)^5+(\frac 1 2)^8+...+(\frac 1 2)^{k}=0.286$
Третьего: $P(B)=(\frac 1 2)^3+(\frac 1 2)^6+(\frac 1 2)^9+...+(\frac 1 2)^{k-2}=0.143$, где $k$ - количество бросаний монеты
И тогда $\frac {P(A)} {P(B)}=\frac {0.286} {0.143}=2$
3) В корабль выпущено два снаряда. Снаряд попадает в цель с вероятностью $\frac 2 3$. При одном попадании корабль утонет с вероятностью $\frac 1 3$, при двух - $\frac 3 4$. Корабль потоплен. Какова вероятность, что в цель попали оба снаряда?
Решение: Составляем гипотезы: $H_1$ - первый снаряд попал в цель
$H_2$ - второй снаряд попал в цель
$H_3$ - оба снаряда попали в цель
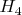
$H_4$ - ни один снаряд не попал в цель
$P(H_1)=P(H_2)=\frac 2 3$
$P(H_3)=\frac 2 3 \cdot \frac 2 3 =\frac 4 9$
$P(H_4)=\frac 1 3 \cdot \frac 1 3 =\frac 1 9$
$A$ - корабль потоплен
$P(A|H_1)=P(A|H_2)=\frac 1 3$
$P(A|H_3)=\frac 3 4$
$P(A|H_4)=0$
И тогда: $P(H_3|A)=\frac 3 7$
4) В поезде два скамьи напротив друг друга по $5$ мест на каждой. Сколькими способами можно разместить $10$ пассажиров, если двое из них будут сидеть напротив друг друга?
Решение: Этих двоих пассажиров можно рассадить $5\cdot2$ способами, оставшихся $8$ пассажиров - $8!$ способами. В итоге, всех пассажиров можно рассадить $5\cdot2\cdot8!$ способами

[faruk]

1. $\checkmark$

2. $\checkmark$ (но некрасиво из-за вычисления десятичных дробей)

3.

ant в сообщении #320729 писал(а):

И тогда: $P(H_3|A)=\frac 3 7$

Каким образом?

4. $\checkmark$

[ValeriaBog]

вероятность попадания двух зарядов $\frac{4}{9}$, а вероятность потопления при этом $\frac{3}{4}$, перемножив получим $\frac{1}{3}$. общая вероятность того, что заряд попал $\frac{7}{9}$. делим $\frac{1}{3}$ на $\frac{7}{9}$, получаем $\frac{3}{7}$- это ответ

[Toucan]

ValeriaBog, Вам объявляется замечание за размещения на форуме решения простой учебной задачи. Читайте правила:

Цитата:

Для тех, кто оказывает помощь в решении задач.
Администрация форума обращается ко всем участникам с убедительной просьбой поддерживать просветительскую функцию раздела, т.е. учить решать задачи. Запрещается публикация полных готовых решений, особенно если речь идет о совсем простых задачах.

(Правильность решения не проверял).

[ant]

faruk, По формуле Байеса:

$$P(H_3|A)=\frac {P(H_3)\cdot P(A|H_3)} {P(H_1)\cdot P(A|H_1)+P(H_2)\cdot P(A|H_2)+P(H_3)\cdot P(A|H_3)+P(H_4)\cdot P(A|H_4)}$$

И после подстановки значений получаем: $P(H_3|A)=\frac 3 7$

[ewert]

ant в сообщении #320729 писал(а):

Составляем гипотезы: $H_1$ - первый снаряд попал в цель
$H_2$ - второй снаряд попал в цель
$H_3$ - оба снаряда попали в цель
$H_4$ - ни один снаряд не попал в цель
$P(H_1)=P(H_2)=\frac 2 3$
$P(H_3)=\frac 2 3 \cdot \frac 2 3 =\frac 4 9$
$P(H_4)=\frac 1 3 \cdot \frac 1 3 =\frac 1 9$

Всё бы замечательно (и дальше действительно всё, кроме ответа, замечательно). Но: Вас не смущает, что сумма вероятностей гипотез не равна единице?...

(Вы неверно сформулировали первые две гипотезы.)

[ant]

ewert Спасибо огромное, я понял! А ведь раньше, я как то считал и сумма гипотез равнялась единице) Вот только как я считал?
Первые две гипотезы нужно переформулировать так:
$H_1$ - первый снаряд попал в цель, а второй снаряд не попал в цель
$H_2$ - второй снаряд попал в цель, а первый снаряд не попал в цель
Тогда:
$P(H_1)=\frac 2 3 \cdot \frac 1 3=\frac 2 9$
$P(H_2)=\frac 1 3 \cdot \frac 2 3=\frac 2 9$
И тогда: $H_1+H_2+H_3+H_4=\Omega$
Тогда ответ: $P(H_3|A)=\frac {9} {13}=0.692$

[ewert]

Теперь верно.

[ant]

Чтобы не создавать новую тему, решил дописать здесь:
На стоянке стоит $12$ машин. $6$ машин отъехало. Найти вероятность того, что $2$ определённых места будут свободны.
Число благоприятных исходов: $C_2^2 \cdot C_{10}^4$ (т.е. $6$ машин отъехало и два определённых места освободилось)
Общее число исходов: $C_{12}^6$
В итоге: $P=\frac {C_2^2 \cdot C_{10}^4} {C_{12}^6}=0.227$
Правильно ли?

[Henrylee]

Да. Только $C^2_2$ незачем приплетать