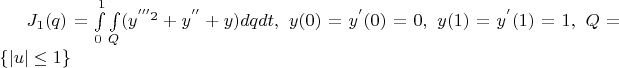Задача про максимум функционала

[asdll]

Здравствуйте! Возникли трудности с решением такой вот задачи
$J_1(q)=\int\limits_0^1\int\limits_Q(y^{'''2} + y^{''} + y)dqdt,\ y(0)=y^{'}(0)=0,\ y(1)=y^{'}(1)=1,\ Q=\{|u|\le1\}$
подскажите плиз, как бы это решить :roll:...
P.S. Кто готов помочь с решением, напишите плиз в лс, с меня вознаграждение!)

[AD]

Тема перемещена из "Помогите решить/разобраться (М)" в карантин. Прежде чем начнётся обсуждение, Вы должны привести Ваше сообщение в соответствие с правилами форума. В частности, все формулы должны быть написаны в $\TeX$е (введение здесь).
Воспользуйтесь кнопкой для редактирования сообщений, а как справитесь - пишите сюда, и тему вернут.

Помощь за деньги на нашем форуме уже отменили.

[AD]

Возвращено.
Ой, я Вам неправильную ссылку подсунул, да?, извиняюсь. Обычно вот сюда пишут, чтобы вернули.

-- Чт май 13, 2010 21:38:17 --

Давайте теперь еще раз, чтобы все поняли. То есть у Вас $q$ - это функция на отрезке $Q$, и Вы минимизируете вот такой интеграл от интеграла Стилтьеса? А тогда что такое $u$?

"Кто на ком стоял? Выражайтесь конкретнее!" (с) кто-то тут недавно цитировал.

[asdll]

извиняюсь, не переписал само условие) вот оно:
Найти структуру вероятностных случайных функций q(u,t), доставляющих глобальный максимум следующим функционалам (вектор u состоит из компонент высших производных), и вот то же выражение, чтоб не скроллить:

[asdll]

Пожалуста, кто хоть представляет что тут, напишите в лс, очень надо поговорить!!

[asdll]

ап

[ИСН]

У Вас написана хрень.

[asdll]

В смысле?? вот если что оригинальное условие

[asdll]

ап!

[VPro]

asdll в сообщении #319986 писал(а):

В смысле?? вот если что оригинальное условие

Да.... Я всякое повидал, но "структура вероятностной случайной функции" и вся эта белиберда, выдаваемая за условие задачи, производит неизгладимое впечатление. Простите, но где ТАКОМУ учат?