Есть отрезок, есть его покрытие: для каждой точки отрезка

есть содержащая его окрестность, т.е. интервал с центром в точке

длины

, где

- положительная, сравнительно легковычислимая функция. Требуется найти минимальное покрытие отрезка.
Задача возникла в процессе решения одного уравнения: в любой точке

может быть найдено его решение в виде ряда, для радиуса сходимости которого выполнена оценка:

.

представляет собой рациональную дробь, только в ней еще присутствуют функции
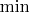
и
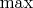
. Надо решить уравнение на отрезке, использовав как можно меньше разложений в ряд.
Пробовал просто "гнать" решение, пробовал находить точку максимума

и удалять ее вместе с окрестностью, искал покрытие в виде пересекающихся только в одной точке отрезков,- полученные результаты не особо вдохновили. Может быть, я просто изобретаю велосипед, а алгоритм решения таких задач известен?
Подскажите, пожалуйста.



