Диссертация, вполне возможно, и годится. Однако ж соединять точечки линеечками -- и впрямь никуда не годится
Иллюстрируя число сочетаний графически, я рисую кривую и объявляю это ломаной. Чтобы предъявлять претензии к обсуждаемому графику, надо знать его роль в тексте, возможно она просто иллюстративна. Не будучи в теме диссартации, не могу быть столь категоричен. Наверное вряд ли, но всё-таки вдруг график и в самом деле является ломаной? Аффтар это даже не обсуждает - считает достаточным доводом против диссертации прикладывание карточки.
Вы про что?
Да вот про
его "оналез" этого
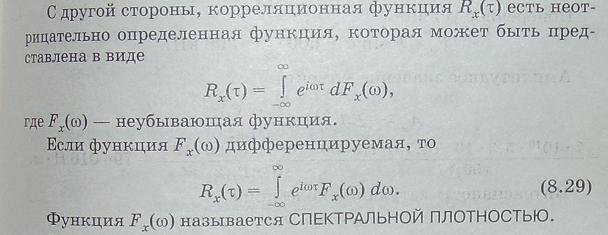
Я не спец в теории групп и никогда бы не взялся за анализ статьи по этой тематике. Идиот я что ли? Но вот добрался до его "оналеза" в этой области и ... пацталом!
kahey писал(а):
И так. Первый спорный вопрос, который у меня возник связан со следующим утверждением (цитирую):
Если не предполагать, что группа конечна, то картеровы подгруппы могут быть даже неизоморфными. Действительно, если N1,N2 _ две неизоморфные нильпотентные группы, то они являются картеровыми подгруппами в своем свободном произведении.
Если бы не было сказано о свободном произведении, то фраза представляла бы собой тофтологию (Действительно, если N1,N2 _ две неизоморфные нильпотентные группы, то они являются картеровыми подгруппами .) и следовательно не представляла бы собой доказательства. Однако было сказано о свободном произведении. Не могу сейчас сказать однозначно что под этим подразумевается, но если речь идёт о преобразовании одномерного пространства в двухмерное, то из мат. анализа известно, что можно взаимооднозначно сопоставить отрезок (интервал) и плоскость.
Таким образом я бы сказал, что приведённое доказательство спорное. Я бы предпочёл конкретный пример ( желательно с доказательством отсутствия изоморфизма).
Если бы не было сказано о свободном произведении, то не было бы указания на группу, в которой группы N1 и N2 являются картеровыми подгруппами. С тем же успехом можно было бы оборвать фразу на слове являются. Вот являются N1 N2 и всё тут, а если бы не явились ... , то возник бы у аффтара вопрос?
Что понимают алгебраисты (и групповики в частности) под свободным произведением - гадать не стоит, если не знаешь, то всё одно не угадаешь. Равномощность интервала и плоскости, преобразования пространств и приплетённый сюда матан связаны с вопросом не больше, чем огородный дядька с киевской бузиной. Аффтару желателен пример? Пусть возьмёт две бесконечные нильпотентные группы разных ступеней нильпотентности, например, группы унитреугольных матриц второго и третьего порядков. Есть у аффтара вопросы по терминам или это опять "тофтология"?
Итак, как ни верти и так и эдак – везде у аффтара туфтология.