Два неравенства

[Sasha2]

Да я уже не знаю как и обращаться к Вам.
Прямо Вы не говорите.
А вот этот Ваш пост,

arqady в сообщении #283181 писал(а):

It must be
$(x+y+z)^3+48(xy+yz+xz)\geq{24(x^2+y^2+z^2)}$
Move on! But I think it's the end.

как его следует расцеивать, как насмешку, или как призыв к попытке доказать это неравенство
$(x+y+z)^3+48(xy+yz+xz)\geq{24(x^2+y^2+z^2)}$

[arqady]

Sasha2 в сообщении #283416 писал(а):

Да я уже не знаю как и обращаться к Вам.
Прямо Вы не говорите.
А вот этот Ваш пост,

arqady в сообщении #283181 писал(а):

It must be
$(x+y+z)^3+48(xy+yz+xz)\geq{24(x^2+y^2+z^2)}$
Move on! But I think it's the end.

как его следует расцеивать, как насмешку, или как призыв к попытке доказать это неравенство
$(x+y+z)^3+48(xy+yz+xz)\geq{24(x^2+y^2+z^2)}$

Попробую восстановить (проверьте!) последовательность постов:

Sasha2 в сообщении #283143 писал(а):

Сокращая на общие члены, получаем, что наше неравенство приводится к виду
$(x+y+z)^3+48(xy+yz+xz)+12(x+y+z)\geq{24(x^2+y^2+z^2)}$
Может подскажите явные ляпы, чтобы уверенно можно было двигаться дальше.

arqady в сообщении #283181 писал(а):

It must be
$(x+y+z)^3+48(xy+yz+xz)\geq{24(x^2+y^2+z^2)}$
Move on! But I think it's the end.

Sasha2 в сообщении #283416 писал(а):

Да я уже не знаю как и обращаться к Вам.
Прямо Вы не говорите.
А вот этот Ваш пост,

arqady в сообщении #283181 писал(а):

It must be
$(x+y+z)^3+48(xy+yz+xz)\geq{24(x^2+y^2+z^2)}$
Move on! But I think it's the end.

как его следует расцеивать, как насмешку, или как призыв к попытке доказать это неравенство
$(x+y+z)^3+48(xy+yz+xz)\geq{24(x^2+y^2+z^2)}$

Расценивать это нужно напрямую, как написано.
Вы просили указать на ошибку, чтобы двигаться дальше?
Это было сделано с замечанием, что, по моему, это не имеет смысла ("Move on! But I think it's the end" )
Теперь скажу Вам окончательно: Ваше неравенство неверно! Например, $x=0$, $y=1$ и $z=12$.

[Sasha2]

Ну тогда и Ваше тоже неверно.
Ведь то к чему мы пришли получается из Вашего неравенства, как прямое следствие.

[arqady]

Sasha2 в сообщении #283600 писал(а):

Ну тогда и Ваше тоже неверно.
Ведь то к чему мы пришли получается из Вашего неравенства, как прямое следствие.

Ваше утверждение неверно. Вы забываете, что между $x,$ $y$ и $z$ есть связь.
Смотрите:
$x+2=\dfrac{a}{b}+\dfrac{b}{a}$, $y+2=\dfrac{b}{c}+\dfrac{c}{b}$ и $z+2=\dfrac{a}{c}+\dfrac{c}{a}$.
Это означает, что $a,$ $b$ и $c$, вообще говоря, можно исключить из этой системы.
Кстати, это легко сделать и получается довольно удобоворимый результат.

[Sasha2]

Стоп, стоп, пожалуйста.
Я только одного не могу понять, как при верных преобразованиях можно от верного неравенства перейти к неверному. Это первое.
И второе, если это так, как Вы говорите, то это означает, что и те два ранее доказанные неравенства не очень то можно считать доказанными, ИБО МЕТОД СОМНИТЕЛЕН. Правильно ли это. Вообще какая-то каша в голове создалась.


А еще меня интересует такой вот вопрос
Ну вот, например если отталкиваться от первого неравенства, зная, что оно заведомо верно
$(a + b + c)\left(\frac {1}{a} + \frac {1}{b} + \frac {1}{c}\right)\geq7 + \sqrt {(a^2 + b^2 + c^2)\left(\frac {1}{a^2} + \frac {1}{b^2} + \frac {1}{c^2}\right) - 5}$,
то можно ли сразу вот неглядя утверждать, что и вот такое будет верно:
$(a + b + c+d)\left(\frac {1}{a} + \frac {1}{b} + \frac {1}{c}+\frac {1}{d}\right)\geq7 + \sqrt {(a^2 + b^2 + c^2+d^2)\left(\frac {1}{a^2} + \frac {1}{b^2} + \frac {1}{c^2}+\frac {1}{d}\right) - 5}$.
А если нет, то имеется ли быстрый и удобный способ нахождения этих 7 и 5, которые фигурируют в исходном неравенстве.
Короче говоря, можно ли все это поставить на алгоритмические рельсы решения, или мы обречены мучиться, кропотливо доказывая каждое неравенство в кажом конкретном случае?

[arqady]

Sasha2 в сообщении #283621 писал(а):

Стоп, стоп, пожалуйста.
Я только одного не могу понять, как при верных преобразованиях можно от верного неравенства перейти к неверному.

Оно неверно вообще и верно при условии, на которое я Вам указал здесь:

Sasha2 в сообщении #283621 писал(а):

И второе, если это так, как Вы говорите, то это означает, что и те два ранее доказанные неравенства не очень то можно считать доказанными, ИБО МЕТОД СОМНИТЕЛЕН. Правильно ли это.

Совсем нет! Ранее доказанные неравенства доказаны, конечно. Просто этот метод пока не помагает для доказательства более хитрых неравенств.
Кстати, Вы ещё не нашли соотношение между $x,$ $y$ и $z$, о котором я Вам всё время напоминаю. Может, найдя его, Вы сможете завершить доказательство моего неравенства методом Полосина.

Sasha2 в сообщении #283621 писал(а):

А еще меня интересует такой вот вопрос
Ну вот, например если отталкиваться от первого неравенства, зная, что оно заведомо верно
$(a + b + c)\left(\frac {1}{a} + \frac {1}{b} + \frac {1}{c}\right)\geq7 + \sqrt {(a^2 + b^2 + c^2)\left(\frac {1}{a^2} + \frac {1}{b^2} + \frac {1}{c^2}\right) - 5}$,
то можно ли сразу вот неглядя утверждать, что и вот такое будет верно:
$(a + b + c+d)\left(\frac {1}{a} + \frac {1}{b} + \frac {1}{c}+\frac {1}{d}\right)\geq7 + \sqrt {(a^2 + b^2 + c^2+d^2)\left(\frac {1}{a^2} + \frac {1}{b^2} + \frac {1}{c^2}+\frac {1}{d}\right) - 5}$.

А зачем неглядя? "неглядя" приводит к ошибкам. И зачем вообще "отталкиваться"? Лучше подумать и доказать. Тем более, очень похоже, что Ваше последнее неравенство верно для положительных $a$, $b$, $c$ и $d$.

Sasha2 в сообщении #283621 писал(а):

А если нет, то имеется ли быстрый и удобный способ нахождения этих 7 и 5, которые фигурируют в исходном неравенстве.

7 и 5 находятся из соображений достижения равенства.
Одно из них, что равенство достигается, когда $a=b=c$.

Sasha2 в сообщении #283621 писал(а):

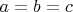
Короче говоря, можно ли все это поставить на алгоритмические рельсы решения, или мы обречены мучиться, кропотливо доказывая каждое неравенство в кажом конкретном случае?

На сегодняшний день такого алгоритма нет и он вряд ли возможен. Реально, в этой области всё происходит именно так, как Вы и описали. Более того, немного изменив известное неравенство можно получить что-то очень трудное для доказательства или (что происходит гораздо чаще) неверное неравенство.

[Sasha2]

Нет Аркадий. Все равно, заранее признавая Ваше превосходство, вижу одно только, что учиться мне еще выше крыши.
А Ваше неравенство я попытаюсь доказать как-нибудь по другому.
Скажем прямо, Вы просто видите сразу то, чего вотя совершенно не вижу.
А вот подскажите куда тут двигаться, чтобы тоже вот так шпарить эти неравенства как Вы.
Так как те неравенства, которые предлагаете Вы, мне даются лишь неоторые (очень малая их часть) и с трудом.
А Вам наверно, раз плюнуть.
Ну как вот такую технику получить. Или я тупой?

[arqady]

Sasha2 в сообщении #283676 писал(а):

А Ваше неравенство я попытаюсь доказать как-нибудь по другому.

Ну и зря! Найдите соотношение между $x$, $y$ и $z$ и Вы его легко докажете! Теперь я вижу, как это сделать.

Sasha2 в сообщении #283676 писал(а):

Ну как вот такую технику получить.

Она вот так и приобретается. Найдите соотношение между $x$, $y$ и $z$ сами и завершите доказательство неравенства. Затем попробуйте доказать его другим способом.
Впечатление от того, что Вы своими руками пощупали, как наш мир устроен, придаст Вам уверенности и силы проделать то же самое с другой задачей и т.д.

[Sasha2]

Имеем
$\frac{a}{b}+\frac{b}{a}=x+2$
$\frac{b}{c}+\frac{c}{b}=y+2$
$\frac{a}{c}+\frac{c}{a}=z+2$

Возводим все три этих равенства в увадрат и складываем. В результате получаем, окончательно:
$\frac{a^2}{b^2}+\frac{b^2}{a^2}+\frac{b^2}{c^2}+\frac{c^2}{b^2}+\frac{a^2}{c^2}+\frac{c^2}{a^2}=x^2+y^2+z^2+4(x+y+z)+6$

Теперь все три перемножаем.
В результате получаем окончательно
$\frac{a^2}{b^2}+\frac{b^2}{a^2}+\frac{b^2}{c^2}+\frac{c^2}{b^2}+\frac{a^2}{c^2}+\frac{c^2}{a^2}+2=(x+2)(y+2)(z+2)$

В конечном счете уже видна связь между x, y и z. Она такая
$x^2+y^2+z^2+4(x+y+z)+6=(x+2)(y+2)(z+2)-2$

Дальше уже неинтересно, поскольку выклатки тривиальны, а конечное неравенство сводится к такому:
$(x+y+z)^3\geq{24xyz}$, что тривиально справедливо, поскольку справедливо и при сомножителе 27, а уж при 24 и подавно.
И все равно остается какая-то неудовлетворенность. Как-то уж слишком все это неестественно.

[arqady]

Sasha2, мои поздравления!
Простите за банальные наставления.

[Sasha2]

И Вам, уважаемый Аркадий, спасибо огромное и за красивые задачи и за науку.