Свойство умножение матриц (AB)C= A(BC).
Док-во.
Если

,

,
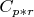
, то элемент

матрицы (AB)C равен

,
А элемент

матрицы A(BC) равен

, но тогда равенство

вытекает из возможности
изменения порядка суммирования относительно j и k.
Вопрос. Что означает фраза "изменение порядка суммирования относительно j и k" ?