13th International Mathematical Competition (IMC) for University Students, Odessa-2006
1st Day, 22 July 2006
1. Let
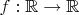
be a real function. Prove or disprove each of the following statements. (a) If

is continuous and
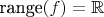
then

is monotonic. (b) If

is monotonic and
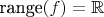
then

is continuous. (c) If

is monotonic and

is continuous then
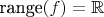
.
2. Find the number of positive integers

satisfying the following two conditions: 1)
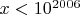
, 2)

is divisible by
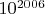
.
3. Let

be an
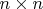
matrix with integer entries and
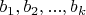
be integers satisfying
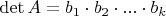
. Prove that there exist
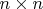
-matrices
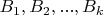
with integers entries such that
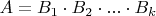
and

for all
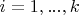
.
4. Let

be a rational function (i.e. the quotient of two real polynomials) and suppose that

is an integer for infinitely many integers

. Prove that

is a polynomial.
5. Let

be five strictly positive real numbers such that

Compare
![\[ a^{3}+b^{3}+c^{3} \] \[ a^{3}+b^{3}+c^{3} \]](https://dxdy-04.korotkov.co.uk/f/3/4/2/34241881fc22cfcac75f99eddf3833d482.png)
with
![\[ d^{3}+e^{3}. \] \[ d^{3}+e^{3}. \]](https://dxdy-03.korotkov.co.uk/f/e/9/a/e9ac8478508a47059fbd5c9e6215fc3082.png)
6. Find all sequences
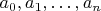
of real numbers such that
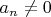
, for which the following statement is true:
If
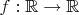
is an

times differentiable function and
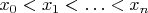
are real numbers such that

then there is
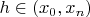
for which
![\[ a_{0}f(h)+a_{1}f'(h)+\ldots+a_{n}f^{(n)}(h)=0. \] \[ a_{0}f(h)+a_{1}f'(h)+\ldots+a_{n}f^{(n)}(h)=0. \]](https://dxdy-03.korotkov.co.uk/f/e/1/7/e17e2b64812a3b99ae1ba9e9d226283b82.png)
General info:
http://www.imc-math.org/index.php?year=2006
Problem 1:
http://www.mathlinks.ro/Forum/viewtopic.php?t=103086
Problem 2:
http://www.mathlinks.ro/Forum/viewtopic.php?t=103090
Problem 3:
http://www.mathlinks.ro/Forum/viewtopic.php?t=103092
Problem 4:
http://www.mathlinks.ro/Forum/viewtopic.php?t=103093
Problem 5:
http://www.mathlinks.ro/Forum/viewtopic.php?t=103089
Problem 6:
http://www.mathlinks.ro/Forum/viewtopic.php?t=103094



