Вот, кстати, ещё одна красивая задача на тему про окружности и четырёхугольники. Не помню, писал я её на этом форуме или ещё нет.
Четырёхугольник

вписан в окружность. Прямые

и

пересекаются в точке

, а прямые

и

--- в точке

. Длина касательной к окружности, проведённой из точки

, равна

, а длина касательной из точки

равна

. Найти длину отрезка
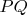
.
Здесь четырёхугольник не описан вокруг окружности, а, наоборот, вписан в неё. Вместа равенства сумм противоположных сторон возникает равенство сумм противоположных углов. И этот-то критерий как раз доказывается просто.
-- Сб дек 26, 2009 12:44:17 --На самом деле это не всегда верно.
Это верно только в том случае, когда вписываемая в четырехугольник окружность лежит внутри него.
Непонятно, как окружность, вписанная в четырёхугольник, может лежать не внутри этого четырёхугольника. Я считаю, что окружность вписана в четырёхугольник, если она касается каждого из четырёх отрезков (не прямых, а именно отрезков), образующих стороны четырёхугольника.
-- Сб дек 26, 2009 12:49:53 --По уже доказанному имеем AB+CD'=AC+AD'.
А также имеем по условию AB+CD=AC+AD.
Дальше по вариации, пересекает ли AD вписанную окружность или нет.
В любом случае, вычитая из равенства AB+CD=AC+AD равенство AB+CD'=AC+AD',
получаем, что AD-AD'=DD', это (AD>AD', перечечения нет) или AD'-AD=DD' (AD'>AD, перечечение есть).
В любом случае получаем, что в треугольнике ADD' одна из сторон равна разности двух других, а этого не может быть.
Тут всё правильно, нигде нет опечаток?
Аналогично и случай, когда четырехугольник невыпуклый. Точно такое же рассуждение показывает, что и обратная теорема верна.
Как можно вписать окружность в не выпуклый четырёхугольник?