Маленькая задачка по теории вычислимости

[Профессор Снэйп]

Достаточно стандартная и простая для специалстов, но для изучающих теорию может показаться интересной.

Как известно, частично рекурсивная функция --- это частичная функция из $\mathbb{N}^k$ в $\mathbb{N}$, получающаяся из базисных (инкремент, ноль и проекции) конечным числом суперпозиций, примитивных рекурсий и минимизаций. По тезису Чёрча (который не доказуем, но в который все верят) функция частично рекурсивна тогда и только тогда, когда она вычислима в самом общем смысле (то есть существует алгоритм её вычисления, то есть вычисление этой функции можно запрограммировать на компьютере с потенциально бесконечной памятью).

Я напомню определение минимизации. Пусть $\bar{x} = x_1, \ldots, x_k$. Говорим, что $f(\bar{x})$ получается минимизацией из $g(y, \bar{x})$ и пишем $f(\bar{x}) = \mu y (g(y,\bar{x}) = 0)$, если для любого $\bar{x} \in \mathbb{N}^k$

$$ f(\bar{x}) = \begin{cases} y_0, & g(y_0,\bar{x}) = 0 \text{ и для любого }y < y_0 \text{ зна-}\\ & \text{чение } g(y, \bar{x}) \text{ определено и не равно } 0;\\ \text{не определено}, &\text{если такого }y_0\text{ не существует}. \end{cases} $$

Иногда говорят, что $f(\bar{x})$ есть минимальный $y$, для которого $g(y,\bar{x})=0$, но в случае, когда $g$ не всюду определена, это может оказаться неверным. К примеру, если $g(0,\bar{x})$ не определено и $g(1,\bar{x})=0$, то $f(\bar{x})$ не определено, несмотря на то, что минимальный $y$, для которого $g(y,\bar{x})=0$, существует и равен $1$.

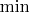
Пусть $\min$, в отличие от оператора минимизации, обозначает настоящий минимум, то есть в предыдущем примере $\min \{ y : g(y, \bar{x}) = 0 \}$ равен $1$.

А теперь сама задача. Привести пример частично рекурсивной функции $g(y,\bar{x})$, такой что функция $h(\bar{x}) = \min \{ y : g(y, \bar{x}) = 0 \}$ не является частично рекурсивной. Другими словами, надо придумать вычислимую функцию, для которой минимальное значение корня этой функции не вычислимо.